跳转到内容
统一场论

低电压变化电磁场产生引力场试验

作者

段落标题 作者

张祥前

  • 交流微信: 18714815159

前言

段落标题 前言

1831年，英国科学家法拉弟实验发现了电感应现象，实现了电与磁的相互转化，人类从此进入电文明时代。

关于电和磁的本质规律人类一直在探索中，爱因斯坦更是用40多年的时间尝试将电磁与引力统一起来，遗憾的是他没有成功。

本人带来的统一场论，是人类首次指出了电磁场和引力场满足的数学关系式。本人在2023年11月2日，第一次试验发现了引力场效应，以后，我一直坚持试验。但是，我使用的电压都是上万伏才能够看到引力场效应。由于高压伴随着静电马达效应、极化效应、离子风效应，难以和引力场效应分清楚，说服力不强。

最近，安徽迪维乐普非晶器材有限公司的徐总在和我合作试验，在我的理论指导下，他们在低电压情况下试验发现变化电磁场产生引力场效应。他们在12伏至160伏低电压情况下，发现了明显的引力场效应，这是自1831年法拉第发现电磁感应以来，人类最重大的科学发现。表明取代电文明的场文明时代已经到来。徐总这个试验已经向国家专利局提交了申请，前几天，国家专利局的受理书已经下来了。

我今天把详细的试验方法公布，有试验能力的网友、高校、科研所，可以重复这个试验。这个试验简单，而且成本不超过一万元。

实验方法

段落标题 实验方法

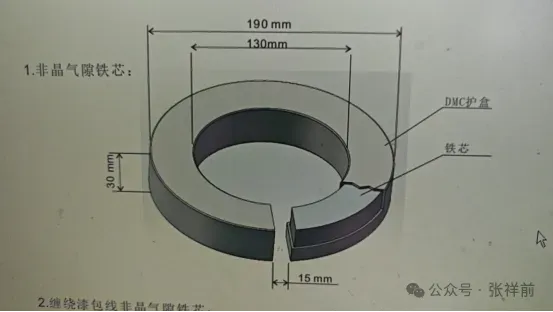
选用非晶材质的软磁环形铁芯【使用普通的厚度 0.2 至 0.5 毫米硅钢片也可以】，该非晶材料饱和磁感应强度 Bs = 1.25 特斯拉（T），磁导率大于等于 100000，铁芯内径130 mm，外径190 mm，厚度30 mm。

在圆环上切开一个15 mm长度的切口，形成一段长15 mm的气隙。在圆环上用直径2mm的漆包铜线绕制400匝的励磁绕组。

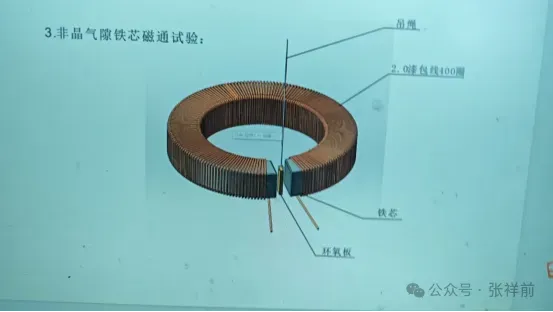
实验的时候，当线圈接通电流 I = 30 A、频率 f = 50 Hz、电压 V = 80 伏的交流电。

在铁芯的气隙处生成一交变磁通，气隙处磁场峰值强度。经过检测约为0.1 至 0.3特斯拉（T）。

在气隙处用细线悬挂的试验材料有：

  1. 环氧树脂板（强绝缘材料）；
  2. 陶瓷；
  3. 塑料；
  4. 不锈钢；
  5. 绿色树叶；
  6. 生鲜的猪肉；
  7. 聚乙烯；
  8. 铝；
  9. 橡胶；
  10. 纸；
  11. 玻璃；
  12. 铜；
  13. 有机玻璃······等其他材料。

线圈通电后，发现可使一切材质的物体发生运动，运动的方向明显与磁力线垂直。

在气隙处，沿磁力线的一个垂直剖面上，取这个剖面的中心点，放置在气隙处的一切材料物体，沿磁力线垂直方向，向这个中心点运动。

这种运动和地球表面产生的引力场令一切物体运动高度类似，我们有理由相信是变化的电磁场产生了引力场。

我们还用12V至80V、电流30A至130A直流电进行过试验，和交流电的情况类似。直流电源可以用电瓶、交流转直流电源。

理论推导

段落标题 理论推导

1. 基本假设

段落标题 1. 基本假设

宇宙任何物体，周围空间总是以矢量光速 C′⃗\vec{C^\prime}【本文大写字母为矢量】、以圆柱状螺旋式向四周发散运动。

在统一场论中，圆柱状螺旋式运动的直线运动部分是电场，旋转运动部分是磁场，旋转指向中心轴线的加速度是引力场，三场相互垂直。

电场

段落标题 电场

当空间在运动的时候，会在前进方向产生电场。 当空间停止运动的时候，电场消失。

磁场

段落标题 磁场

当空间在运动的时候，会在旋转的切线方向产生磁场。当空间停止旋转运动，磁场消失。

引力场

段落标题 引力场

当空间在螺旋运动的时候，有一个指向中心的加速度，这个就是引力场，当空间停止旋转运动，引力场消失。

静止物体周围也有磁场，只是在一个曲面上有多少磁场线穿进去，就有多少磁场线穿出来，相互抵消了，对外不显效应。

以上基本假设提到了空间本身在运动。

为了描述空间本身的运动，我们把空间分割成许多个小块，每一个小块叫空间点，通过描述空间点的运动，就可以描述空间本身的运动。

以上基本假设提到了矢量光速。

本文认为光速可以扩展到矢量，矢量光速的方向可以变化，模是标量光速，用小写字母 cc 表示，cc 不变。

当物体粒子 oo 点相对于我们观察者静止，周围一个空间点 pp 以矢量光速 C′⃗\vec{C^\prime} 向四周发散运动，当 oo 点以速度 V⃗\vec{V} 相对于我们运动，pp 点相对于我们观察者的速度我们用矢量光速 C⃗\vec{C} 表示。

C′⃗\vec{C^\prime} 和 C⃗\vec{C} 大小相等，方向不同。C′⃗\vec{C^\prime} 和 C⃗\vec{C} 的关系是否符合相对论的洛伦茨变换？

按照洛伦茨的速度变换，C′⃗\vec{C^\prime} 的三个分量 C⃗x′,C⃗y′,C⃗z′\vec{C}x^{\prime}, \vec{C}y^{\prime} , \vec{C}z^{\prime} 和 C⃗\vec{C} 的三个分量 C⃗x,C⃗y,C⃗z\vec{C}x, \vec{C}y, \vec{C}z 满足的关系为：

C⃗x′=(C⃗x−v)[1−(C⃗xvc2)]\vec{C}x^{\prime} = \dfrac{(\vec{C}x - v)}{[1 - (\vec{C}x \dfrac{v}{c²})]} C⃗y′=[C⃗y(1−v2c2)][1−(C⃗xvc2)]\vec{C}y^{\prime} = \dfrac{[\vec{C}y \sqrt{(1 - \dfrac{v²}{c²})}]}{[1 - (\vec{C}x \dfrac{v}{c²})]} C⃗z′=[C⃗z(1−v2c2)][1−(C⃗xvc2)]\vec{C}z^{\prime} = \dfrac{[\vec{C}z \sqrt{(1 - \dfrac{v²}{c²})}]}{[1 - (\vec{C}x \dfrac{v}{c²})]}

由以上可以导出：

(C⃗x′)2+(C⃗y′)2+(C⃗y′)2(\vec{C}x^{\prime})^2 + (\vec{C}y^{\prime})^2 + (\vec{C}y^{\prime})^2 =[(C⃗x−v)2+C⃗y2(1−v2c2)+C⃗z2(1−v2c2)][1−(C⃗xvc2)]2= \dfrac{[(\vec{C}x - v)²+ \vec{C}y²(1 - \dfrac{v²}{c²}) + \vec{C}z²(1 - \dfrac{v²}{c²})]}{[1 - (\vec{C}x \dfrac{v}{c²})]²} =c2c2[C⃗x2+C⃗y2+C⃗z2−2C⃗xv+v2−(c2−C⃗x2)v2c2](c2−C⃗xv)2= c²c² \dfrac{[\vec{C}x²+ \vec{C}y²+ \vec{C}z²-2 \vec{C}x v+ v²-(c²-\vec{C}x²)\dfrac{v²}{c²}]}{(c²-\vec{C}x v)²} =c2c2[c2−2C⃗xv+v2−(c2−C⃗x2)v2c2](c2−C⃗xv)2= c²c²\dfrac{[c²-2 \vec{C}x v+ v²-(c²-\vec{C}x²)\dfrac{v²}{c²}]}{(c²-\vec{C}x v)²} =c2[c2c2−2c2C⃗xv+C⃗x2v2](c2−C⃗xv)2= c² \dfrac{[c²c²-2 c²\vec{C}x v+ \vec{C}x²v²]}{(c²-\vec{C}x v)²} =c2= c²

由此导出矢量光速 C⃗\vec{C} 和 C′⃗\vec{C^{\prime}} 满足以下关系：

C′⃗⋅C′⃗=C⃗⋅C⃗=c2\vec{C^\prime}·\vec{C^\prime} = \vec{C}·\vec{C} = c^2

C⃗\vec{C} 和 C′⃗\vec{C^\prime} 方向不一样，但是，数量是一样的。

当 oo 点相对于我们观察者以速度 V⃗\vec{V} 运动的时候，设空间点 pp 点相对于 oo 点的速度为 U⃗\vec{U}，由于 C⃗\vec{C} 是 U⃗\vec{U} 和 V⃗\vec{V} 的合成，也就是 C⃗\vec{C} = U⃗\vec{U} + V⃗\vec{V}，

所以：

U⃗\vec{U} = C⃗\vec{C} - V⃗\vec{V}

2. 认识引力场

段落标题 2. 认识引力场

我们站在地球上，随手放下一块石头，石头以加速度自由落体向地球中心坠落。

如果没有石头，石头所在的空间仍然以那种方式在向地球中心坠落，这个就是引力场的本质。

引力场的本质就是物体周围空间本身向物体质心加速运动的加速度。

引力场有两个重要的性质：

由物体指向引力场中的一点【我们叫场点，或者叫考察点】的位置矢量，与引力场方向相反。

引力场可以对一切材料构成的物体有加速作用。

3. 认识磁场

段落标题 3. 认识磁场

人类发现，带电粒子相对于我们观察者以匀速直线运动引起运动速度垂直方向的电场变化，电场变化部分可以认为就是磁场，也就是随速度变化的电场产生磁场。

在下图中，一个相对于我们静止的正电荷粒子 oo 点，在周围空间点 pp 处产生了静电场 E′⃗\vec{E^\prime}。当 oo 点相对于我们观察者以速度 V⃗\vec{V} 沿 xx 轴正方向匀速直线运动，可以产生磁场 B⃗\vec{B}。

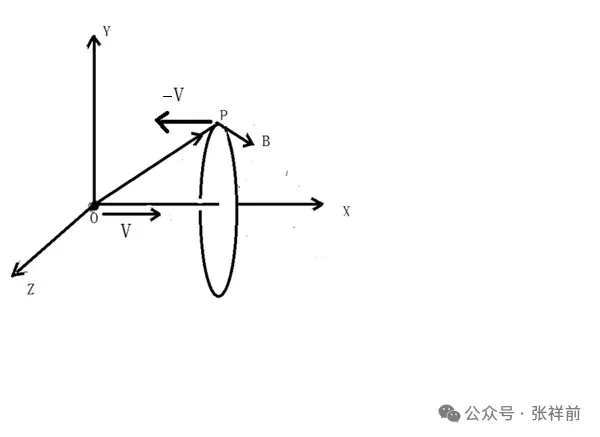
这个磁场的本质就是空间以矢量速度 V⃗\vec{V} 为中心轴线在旋转，B⃗\vec{B} 的旋转和 V⃗\vec{V} 满足右手螺旋关系。

B⃗=V⃗⋅E⃗c2\vec{B} = \vec{V} · \dfrac{\vec{E}}{c^2}

按照矢量叉乘和斯托克斯定理排列顺序的习惯，yy 叉乘以 zz 形成了 xx 方向上的矢量面元，zz 叉乘以 xx 形成了沿 yy 方向的矢量面元，xx 叉乘以 yy 形成了沿 zz 方向的矢量面元，三个分量满足以下右手螺旋关系：

Bx⃗=0\vec{B_x} = 0 By⃗=−V⃗⋅Ez⃗c2\vec{B_y} = -\vec{V} · \dfrac{\vec{E_z}}{c^2} Bz⃗=V⃗⋅Ey⃗c2\vec{B_z} = \vec{V} · \dfrac{\vec{E_y}}{c^2}

oo 点是正电荷，Ez⃗\vec{E_z} 是 oo 点产生的正电场沿 zz 轴的分量，Ey⃗\vec{E_y} 是 yy 轴上的分量。oo 点产生的正电场由 oo 点指向 pp 点。

oo 点产生的正电场由 oo 点指向 pp 点。

由前面的基本假设，oo 点以速度 V⃗\vec{V} 沿 xx 轴正方向运动的时候，空间点 pp 正好有一个相反的速度 −V⃗- \vec{V}。

如果我们把考察点从 oo 点上移开，考察点设定在空间的 pp 点上，则以上右手螺旋关系要改成左手螺旋关系：

Bx⃗=0\vec{B_x} = 0 By⃗=V⃗⋅Ez⃗c2\vec{B_y} = \vec{V} · \dfrac{\vec{E_z}}{c^2} Bz⃗=−V⃗⋅Ey⃗c2\vec{B_z} = - \vec{V} · \dfrac{\vec{E_y}}{c^2}

当我们考察分析空间某处 pp 点的运动情况，用这个分量公式更直接方便。

4. 随时间变化的磁场产生电场和引力场

段落标题 4. 随时间变化的磁场产生电场和引力场

在统一场论中，引力场 A⃗\vec{A} 的旋度和均匀磁场 B⃗\vec{B} 所满足以下关系：

∇⃗⋅A⃗=1fB⃗\vec{\nabla} · \vec{A} = \dfrac{1}{f} \vec{B}

式中的 ff 是常数。这个是磁场和引力场满足的基本关系方程，这个方程告诉我们，电荷以某一个速度匀速直线运动时候产生的磁场，可以表现为引力场的旋度形式。

电磁学和量子力学引入的磁矢势概念，并非是一个虚无的概念，其本质就是漩涡引力场。这个方程可能是量子力学中AB效应的最终解释。

将以上方程两边点乘矢量面元 【可以看成是包围电荷粒子 oo 点的高斯球面 s=4πr2s = 4πr² 上一小块面积，其正方向，也就是法方向向外】，再利用场论中的斯托克斯定理，可以得到磁场和引力场之间关系的满足积分方程：

∮A⃗⋅dl⃗=1f∯B⃗⋅dS⃗\oint \vec{A} ·d\vec{l} = \dfrac{1}{f} \oiint \vec{B} · d \vec{S}

这种引力场以磁力线为轴线，满足右手螺旋，在空间中环绕分布。

接下来，我们考虑磁场 B⃗\vec{B} 的变化情况。

设想一个正点电荷 oo 点，在 00 时刻从笛卡尔坐标的原点出发，相对于我们观测者以速度 【标量为 vv 】沿 xx 轴正方向匀速直线运动。

在参考系 ss 系【 s′s^\prime 系相对于 ss 系以匀速度沿 xx 轴正方向直线运动】里，点电荷 oo 在周围空间点 pp 处产生了电场 E⃗\vec{E}、磁场 B⃗\vec{B}，的环绕是右手螺旋。如下图。

如果我们不以电荷 oo 点作为考察点，而是以空间点 pp 为考察点，由于 oo 点的运动速度 V⃗\vec{V} 和 pp 点的运动速度 −V⃗- \vec{V} 方向正好相反，所以，这里的运动电场 E⃗\vec{E}、均匀磁场 B⃗\vec{B} 满足左手螺旋关系式：

B⃗=−1c2v⃗⋅E⃗\vec{B} = - \dfrac{1}{c^2} \vec{v} · \vec{E}

分量形式为：

Bx⃗=0\vec{B_x} = 0 By⃗=vc2⋅Ez⃗\vec{B_y} = \dfrac{v}{c^2} · \vec{E_z} Bz⃗=−vc2⋅Ey⃗\vec{B_z} = - \dfrac{v}{c^2} · \vec{E_y}

将以上方程 B⃗=−1c2v⃗⋅E⃗ \vec{B} = - \dfrac{1}{c^2} \vec{v} · \vec{E} 对时间 tt 求导数，有：

dB⃗dt=−1c2dv⃗dt⋅E⃗−1c2v⃗⋅dE⃗dt\dfrac{d \vec{B}}{dt} = - \dfrac{1}{c^2} \dfrac{d\vec{v}}{dt} · \vec{E} - \dfrac{1}{c^2} \vec{v} · \dfrac{d\vec{E}}{dt}

如果我们能够证明上式后部分表示的是磁场变化产生变化的电场【也称漩涡电场】，就是法拉第电磁感应原理，作为对应，多出的前一项 应该是变化磁场产生引力场。

因为 dvdt\dfrac{dv}{dt} 是空间点 pp 的加速度，按照统一场论的思想，空间本身的加速度等价于引力场。

我们先来证明上式的后部分就是法拉第电磁感应原理。

三个分量如下【微分号 dd 改为偏微分号 ∂\partial 】：

∂Bx⃗∂t=0\dfrac{\partial \vec{B_x}}{\partial t} = 0 ∂By⃗∂t=vc2∂Ez⃗∂t\dfrac{\partial \vec{B_y}}{\partial t} = \dfrac{v}{c^2} \dfrac{\partial \vec{E_z}}{\partial t} ∂Bz⃗∂t=−vc2∂Ey⃗∂t\dfrac{\partial \vec{B_z}}{\partial t} = - \dfrac{v}{c^2} \dfrac{\partial \vec{E_y}}{\partial t}

由静电场旋度为零

∂Ex′⃗∂z′−∂Ez′⃗∂x′=0\dfrac{\partial \vec{E_x^{\prime}}}{\partial z{^\prime}} - \dfrac{\partial \vec{E_z^{\prime}}}{\partial x{^\prime}} = 0

和洛伦兹正变换

Ex⃗=Ex′⃗,∂z′=∂z,Ez′⃗=1γEz⃗,\vec{E_x} = \vec{E_x^{\prime}}, \partial z^{\prime} = \partial z, \vec{E_z^{\prime}} = \dfrac{1}{\gamma} \vec{E_z}, ∂∂x′=1γ∂∂x,γ=11−v2c2\dfrac{\partial}{ \partial x{^\prime}} = \dfrac{1}{\gamma} \dfrac{\partial}{\partial x}, \gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}

得到：

∂Ex⃗∂z−1γ2∂Ez⃗∂x=0\dfrac{\partial \vec{E_x}}{\partial z} - \dfrac{1}{\gamma^2} \dfrac{\partial \vec{E_z}}{\partial x} = 0

所以

∂Ex⃗∂z−(1−v2c2)∂Ez⃗∂x=0\dfrac{\partial \vec{E_x}}{\partial z} - \left( 1 - \dfrac{v^2}{c^2} \right) \dfrac{\partial \vec{E_z}}{\partial x} = 0

由速度的定义得：

∂Ex⃗∂z−∂Ez⃗∂x=−vc2∂Ez⃗∂t\dfrac{\partial \vec{E_x}}{\partial z} - \dfrac{\partial \vec{E_z}}{\partial x} = - \dfrac{v}{c^2} \dfrac{\partial \vec{E_z}}{\partial t}

类似以上的操作，可以得到：

∂Ey⃗∂x−∂Ex⃗∂y=vc2∂Ey⃗∂t\dfrac{\partial \vec{E_y}}{\partial x} - \dfrac{\partial \vec{E_x}}{\partial y} = \dfrac{v}{c^2} \dfrac{\partial \vec{E_y}}{\partial t}

把这两个式子和上面的 的三个分量：对比，可以得到：

∂Ez⃗∂y−∂Ey⃗∂z=0\dfrac{\partial \vec{E_z}}{\partial y} - \dfrac{\partial \vec{E_y}}{\partial z} = 0 ∂Ex⃗∂z−∂Ez⃗∂x=−∂By⃗∂t\dfrac{\partial \vec{E_x}}{\partial z} - \dfrac{\partial \vec{E_z}}{\partial x} = - \dfrac{\partial \vec{B_y}}{\partial t} ∂Ey⃗∂x−∂Ex⃗∂y=−∂Bz⃗∂t\dfrac{\partial \vec{E_y}}{\partial x} - \dfrac{\partial \vec{E_x}}{\partial y} = - \dfrac{\partial \vec{B_z}}{\partial t}

合并以上三式，正是法拉第电磁感应方程：

∇⃗⋅E⃗=−∂B⃗∂t\vec{\nabla} · \vec{E} = - \dfrac{\partial \vec{B}}{\partial t}

展开分析。

对这个方程可以理解为：

磁场 B⃗\vec{B} 随时间 tt 变化，可以产生电场 E⃗\vec{E} 和引力场 A⃗\vec{A}，并且，在空间某一个点上，B⃗\vec{B}、A⃗\vec{A}、E⃗\vec{E} 三者相互垂直。

以上的试验，在气隙处，一切物体沿磁力线垂直方向运动，证实了这一点。

编辑本页内容 翻译本页内容
贡献 社区