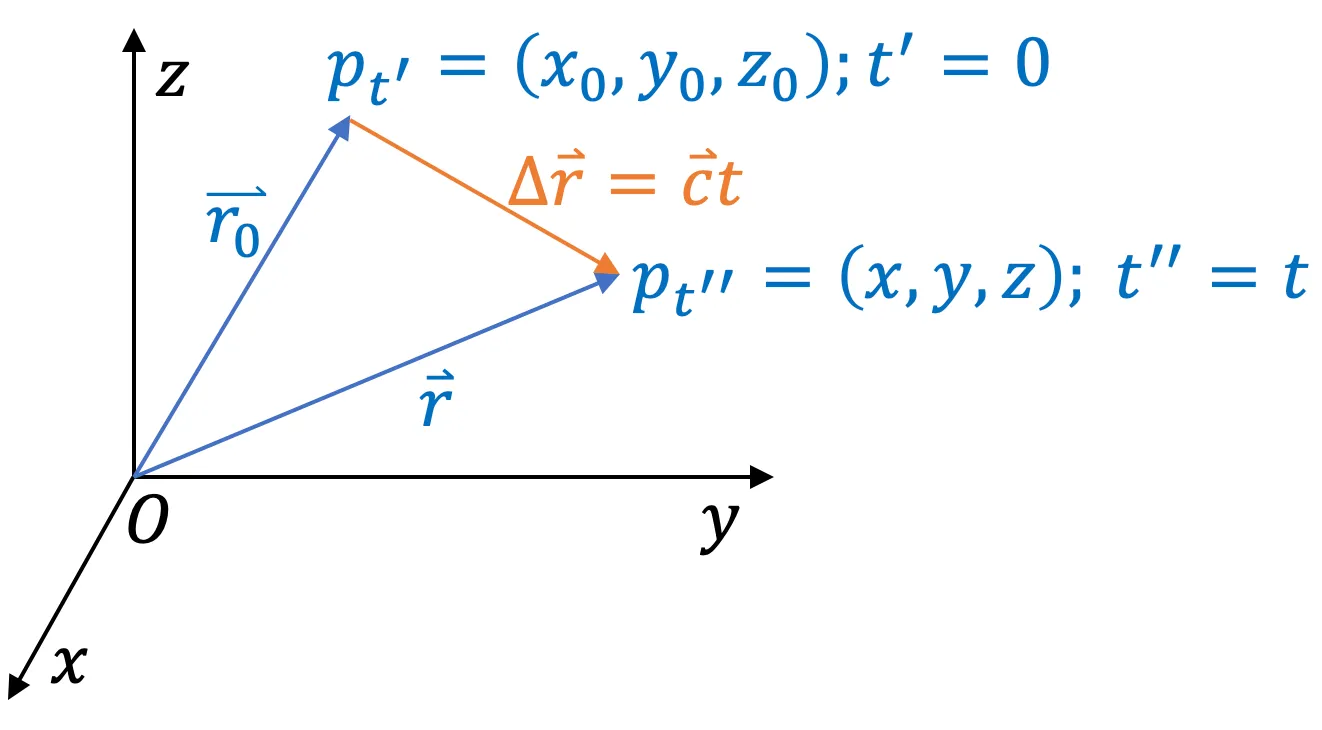以上提到:宇宙中所有的物体【或者叫质点】包括空间本身都是以圆柱状螺旋式在运动,螺旋运动规律是宇宙最基本的规律之一。
统一场论认为物体周围空间本身也是以圆柱状螺旋式在运动。
下面我们来建立统一场论中的三维圆柱状螺旋时空方程,来替代相对论中四维时空方程。
点击展开注解: 关于本书中变量命名问题的说明 点击收起配图 设想在某处空间区域里存在着一个质点 o o o o o o x , y , z x,y,z x , y , z
在时刻 t ′ = 0 t' = 0 t ′ = 0 o o o p p p x 0 , y 0 , z 0 x_0, y_0, z_0 x 0 , y 0 , z 0 o o o p p p r 0 ⃗ \vec{r_0} r 0
p p p t t t t ′ ′ t'' t ′′ p p p x , y , z x, y, z x , y , z p p p t ′ ′ t'' t ′′ x , y , z x, y, z x , y , z o o o p p p r ⃗ \vec{r} r
在圆柱状螺旋式运动中,可以分解为旋转运动矢量和直线运动矢量,注意,不能把位矢和直线运动混淆,位矢可以看成是旋转运动矢量和直线运动矢量的合成。
按照以上的垂直原理,r ⃗ \vec{r} r x , y , z x, y, z x , y , z t t t
r ⃗ ( t ) = ( x , y , z ) \begin{equation}\nonumber
\vec{r}(t) = (x, y, z)
\end{equation} r ( t ) = ( x , y , z ) 点击展开注解: 关于 r ⃗ \vec{r} r x , y , z , t x, y, z, t x , y , z , t
”r ⃗ \vec{r} r x , y , z x, y, z x , y , z t t t r ⃗ \vec{r} r x , y , z , t x, y, z, t x , y , z , t r ⃗ = f ( x , y , z , t ) \vec{r}=f(x, y, z, t) r = f ( x , y , z , t )
给出了 r ⃗ ( t ) \vec{r}(t) r ( t ) ( x , y , z ) (x, y, z) ( x , y , z )
r ⃗ ( t ) = r 0 ⃗ + c ⃗ t = ( x 0 + x ) i ⃗ + ( y 0 + y ) j ⃗ + ( z 0 + z ) k ⃗ \begin{equation}\nonumber
\vec{r}(t) = \vec{r_0}+\vec{c}t = (x_0 + x)\vec{i} + (y_0 + y)\vec{j} + (z_0 + z)\vec{k}
\end{equation} r ( t ) = r 0 + c t = ( x 0 + x ) i + ( y 0 + y ) j + ( z 0 + z ) k 点击展开公式修正
这里将原著上述公式中 x , y , z x, y, z x , y , z Δ \Delta Δ
修正后公式: (其中 Δ x = x − x 0 , Δ y = y − y 0 , Δ z = z − z 0 \Delta x = x - x_0,\ \Delta y = y - y_0,\ \Delta z = z - z_0 Δ x = x − x 0 , Δ y = y − y 0 , Δ z = z − z 0
r ⃗ ( t ) = r 0 ⃗ + c ⃗ t = ( x 0 + Δ x ) i ⃗ + ( y 0 + Δ y ) j ⃗ + ( z 0 + Δ z ) k ⃗ \begin{equation}\nonumber
\vec{r}(t) = \vec{r_0}+\vec{c}t = (x_0 + \Delta x)\vec{i} + (y_0 + \Delta y)\vec{j} + (z_0 + \Delta z)\vec{k}
\end{equation} r ( t ) = r 0 + c t = ( x 0 + Δ x ) i + ( y 0 + Δ y ) j + ( z 0 + Δ z ) k 这个方程有时候也可以简写为:
点击展开注解:此处“简写”的含义
这里简写的含义是, 以空间点 p p p r 0 ⃗ = ( 0 , 0 , 0 ) \vec{r_0}=(0, 0, 0) r 0 = ( 0 , 0 , 0 )
r ⃗ ( t ) = c ⃗ t = x i ⃗ + y j ⃗ + z k ⃗ \begin{equation}\nonumber
\vec{r}(t) = \vec{c}t = x \vec{i} + y \vec{j} + z \vec{k}
\end{equation} r ( t ) = c t = x i + y j + z k 标量形式:
r 2 = c 2 t 2 = x 2 + y 2 + z 2 \begin{equation}\nonumber
r^{2} = c^{2}t^{2} = x^{2} + y^{2} + z^{2}
\end{equation} r 2 = c 2 t 2 = x 2 + y 2 + z 2 r r r r ⃗ \vec{r} r
点击收起动画 点击展开疑问
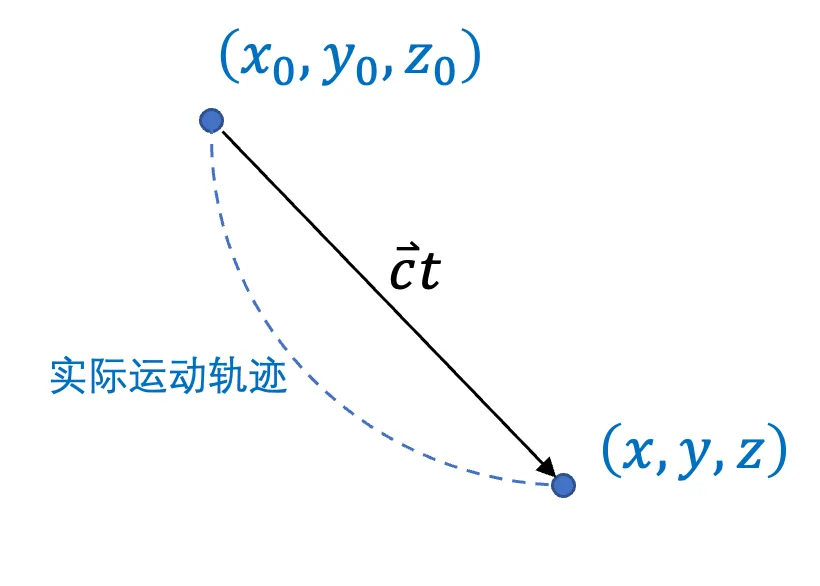
如果一个空间点花费时间 t t t ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) ( x 0 , y 0 , z 0 ) ( x , y , z ) (x,y,z) ( x , y , z ) ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) ( x 0 , y 0 , z 0 ) ( x , y , z ) (x,y,z) ( x , y , z ) c t ct c t ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) ( x 0 , y 0 , z 0 ) ( x , y , z ) (x,y,z) ( x , y , z ) c t ct c t
或许这里不能用惯常的 “位移=速度×时间” 来理解空间的运动, 因为统一场论中本身就是用空间运动来定义时间的。
以上方程在相对论中也出现过,相对论中被认为是四维时空距离,真实情况是时间的本质就是我们对光速运动的空间的描述。三维空间中任意一维以光速运动,我们就可以认为是时间。
空间的存在是基本的,时间不是基本的,没有人这个观察者,时间是不存在的,但是仍然存在着空间。
由于时间是我们观察者对光速运动空间的描述,时间的量等价于光速运动的空间位移量。
相对论显然没有认识到这一点,相对论不知道时间的本质,把时间看成和空间平权的另外一维,和三维空间并列为四维时空。
相对论没有认识到空间是基本的、真实存在的,脱离我们观察者仍然存在,时间是人描述出来的,时间的存在是虚假的,脱离我们观察者是不存在的。
在这方面的认识明显是相对论有缺陷。
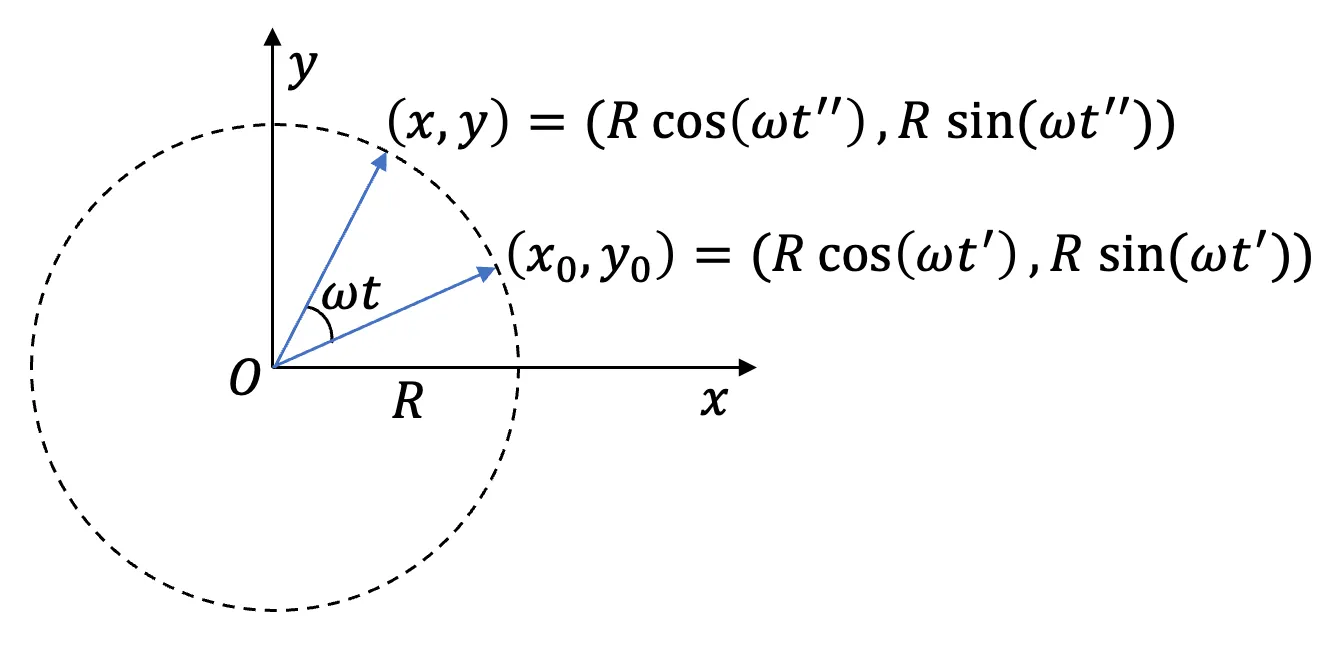
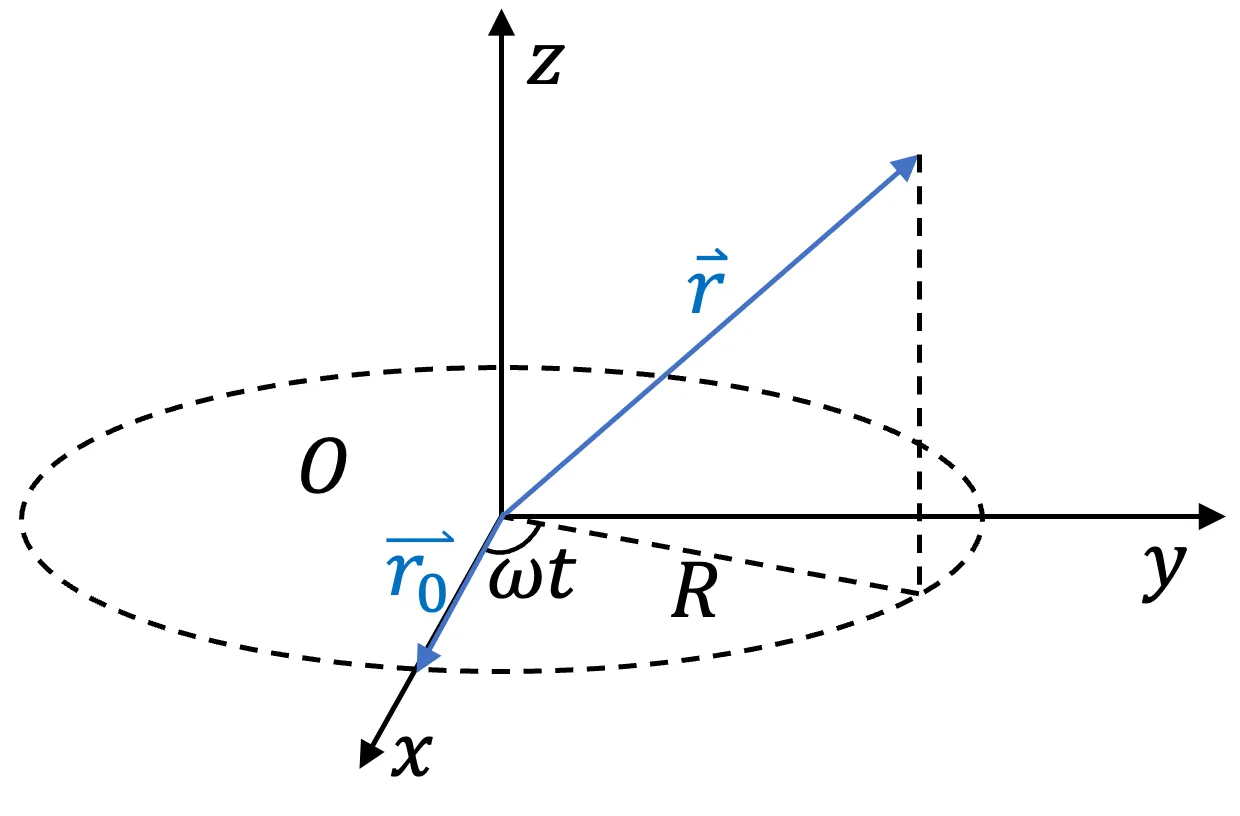
如果 p p p X O Y XOY XO Y ω \omega ω z z z h h h r ⃗ \vec{r} r x x x y y y R R R
点击收起配图
X O Y XOY XO Y
x = x 0 + R c o s ( ω t ) y = y 0 + R s i n ( ω t ) z = z 0 + h t \begin{align}
x =& x_0 + R\ cos(\omega t) \nonumber \\
y =& y_0 + R\ sin(\omega t) \nonumber \\
z =& z_0 + h t \nonumber
\end{align} x = y = z = x 0 + R cos ( ω t ) y 0 + R s in ( ω t ) z 0 + h t 点击展开公式修正
原著中完整形式的 “三维螺旋时空方程” 是有问题的, 我对它进行了修正
修正后公式: (其中 t ′ t' t ′ r 0 ⃗ = ( x 0 , y 0 , z 0 ) \vec{r_0}=(x_0, y_0, z_0) r 0 = ( x 0 , y 0 , z 0 ) t ′ ′ t'' t ′′ r ⃗ = ( x , y , z ) \vec{r}=(x, y, z) r = ( x , y , z ) t ′ ′ − t ′ = t t'' - t' = t t ′′ − t ′ = t
x = x 0 + R ( c o s ( ω t ′ ′ ) − c o s ( ω t ′ ) ) y = y 0 + R ( s i n ( ω t ′ ′ ) − s i n ( ω t ′ ) ) z = z 0 + h t \begin{align}
x =& x_0 + R(cos(\omega t'') - cos(\omega t')) \nonumber \\
y =& y_0 + R(sin(\omega t'') - sin(\omega t')) \nonumber \\
z =& z_0 + h t \nonumber
\end{align} x = y = z = x 0 + R ( cos ( ω t ′′ ) − cos ( ω t ′ )) y 0 + R ( s in ( ω t ′′ ) − s in ( ω t ′ )) z 0 + h t 可以明显看出, 原著公式的错误在于, 误认为 c o s ( A ) − c o s ( B ) = c o s ( A − B ) cos(A) - cos(B) = cos(A-B) cos ( A ) − cos ( B ) = cos ( A − B )
以上也可以用以下矢量方程表示,
r ⃗ = r 0 ⃗ + c ⃗ t = ( x 0 + R c o s ( ω t ) ) i ⃗ + ( y 0 + R s i n ( ω t ) ) j ⃗ + ( z 0 + h t ) k ⃗ \begin{equation} \tag{19.1}
\begin{aligned}
\vec{r}=& \vec{r_0} + \vec{c}t \\
=& (x_0 + R\ cos(\omega t))\vec{i} + (y_0 + R\ sin(\omega t))\vec{j} + (z_0+ht)\vec{k}
\end{aligned}
\end{equation} r = = r 0 + c t ( x 0 + R cos ( ω t )) i + ( y 0 + R s in ( ω t )) j + ( z 0 + h t ) k ( 19.1 ) 点击展开公式修正
修正后公式: (其中 t ′ t' t ′ r 0 ⃗ = ( x 0 , y 0 , z 0 ) \vec{r_0}=(x_0, y_0, z_0) r 0 = ( x 0 , y 0 , z 0 ) t ′ ′ t'' t ′′ r ⃗ = ( x , y , z ) \vec{r}=(x, y, z) r = ( x , y , z ) t ′ ′ − t ′ = t t'' - t' = t t ′′ − t ′ = t
r ⃗ = r 0 ⃗ + c ⃗ t = { x 0 + R [ c o s ( ω t ′ ′ ) − c o s ( ω t ′ ) ] } i ⃗ + { y 0 + R [ s i n ( ω t ′ ′ ) − s i n ( ω t ′ ) ] } j ⃗ + ( z 0 + h t ) k ⃗ \begin{equation} \nonumber
\begin{aligned}
\vec{r} =& \vec{r_0} + \vec{c}t \\
=& \{x_0 + R[cos(\omega t'') - cos(\omega t')]\} \vec{i} + \{y_0 + R[sin(\omega t'') - sin(\omega t')]\} \vec{j} \\
& + (z_0+ht)\vec{k}
\end{aligned}
\end{equation} r = = r 0 + c t { x 0 + R [ cos ( ω t ′′ ) − cos ( ω t ′ )]} i + { y 0 + R [ s in ( ω t ′′ ) − s in ( ω t ′ )]} j + ( z 0 + h t ) k 以上可以叫三维螺旋时空方程。
有时候这个方程可以简化为:
r ⃗ = R c o s ( ω t ) i ⃗ + R s i n ( ω t ) j ⃗ + h t k ⃗ \begin{equation}\nonumber
\vec{r} = R \ cos(\omega t)\vec{i} + R \ sin(\omega t)\vec{j} + ht\vec{k}
\end{equation} r = R cos ( ω t ) i + R s in ( ω t ) j + h t k 点击展开注解:此处“简化”的含义 统一场论认为,宇宙的一切奥妙都是以上方程决定的,大到银河系、星球,小到电子、质子、中子的运动,以及物体为什么有质量、为什么有电荷,一直到人的思维等等······,都与这个方程有关。
三维螺旋时空方程中,旋转运动和直线运动有什么关系呢?
沿坐标 x , y x, y x , y X \mathbf{X} X Y \mathbf{Y} Y z z z Z \mathbf{Z} Z
X × Y = Z Y × X = − Z \begin{align}
\mathbf{X} \times \mathbf{Y} =& \mathbf{Z} \nonumber \\
\mathbf{Y} \times \mathbf{X} =& - \mathbf{Z} \nonumber
\end{align} X × Y = Y × X = Z − Z 上式 X \mathbf{X} X Y \mathbf{Y} Y X × Y = Z \mathbf{X} \times \mathbf{Y} = \mathbf{Z} X × Y = Z Y × X = − Z \mathbf{Y} \times \mathbf{X} = - \mathbf{Z} Y × X = − Z
点击展开疑问:应该都是表示右手螺旋关系吧? 式 X × Y = Z \mathbf{X} \times \mathbf{Y} = \mathbf{Z} X × Y = Z Y × X = − Z \mathbf{Y} \times \mathbf{X} = - \mathbf{Z} Y × X = − Z
这个两个公式来源于前面的“平行原理”和“垂直原理”。
“平行原理”指出,两个物理量如果可以用线段表示的,相互平行的话,一定是正比关系。
“垂直原理”指出了平面或者曲面的方向在其垂直方向上。
而圆周运动的方向在圆周平面垂直方向上,背后的原因也是“垂直原理”。
在式 X × Y = Z \mathbf{X} \times \mathbf{Y} = \mathbf{Z} X × Y = Z X × Y \mathbf{X} \times \mathbf{Y} X × Y X × Y \mathbf{X} \times \mathbf{Y} X × Y X \mathbf{X} X Y \mathbf{Y} Y Z Z Z
按照平行原理,矢量面积 X × Y \mathbf{X} \times \mathbf{Y} X × Y Z \mathbf{Z} Z X × Y = Z \mathbf{X} \times \mathbf{Y} = \mathbf{Z} X × Y = Z
对于以上的三维螺旋时空方程,我们需要注意以下几点:
o o o p p p ( 19.1 ) (19.1) ( 19.1 ) o o o r ⃗ \vec{r} r o o o o o o
螺旋线产生于质点,终结于质点,在没有质点的空间中,不会无缘无故的出现。
o o o
空间的圆柱状螺旋式运动是直线运动和旋转运动两种运动的叠加。也可以认为直线运动是以上提到的圆柱状螺旋式运动中 R = 0 R = 0 R = 0
圆柱状螺旋式方程中所描述的是:空间位矢 r ⃗ \vec{r} r o o o p p p p p p r ⃗ \vec{r} r
空间点 p p p o o o o o o
螺旋方程 ( 19.1 ) (19.1) ( 19.1 ) x x x y y y z z z x x x y y y p p p x x x y y y z z z
将螺旋运动方程对时间求导数,得到了了矢量光速,不能理解为只是将圆柱状螺旋式运动的直线部分对时间求导数而获得的,因为这样就出现超光速了。而是将位矢 r ⃗ \vec{r} r t t t
一个空间点对应一条螺旋线,螺旋半径是 0 0 0
质点 o o o o o o o o o
Learn