在统一场论中,磁场和电场不是同一种场,二者不能直接相互作用,不能直接叠加。
人类已经发现,带电粒子相对于我们观察者以匀速直线运动的时候,可以引起电场的变化,电场变化的部分我们可以认为就是磁场,也就是随速度变化的电场产生了磁场,统一场论继承这种看法。
设想在惯性参照系 s ′ s' s ′ o o o m ′ m' m ′ v ⃗ \vec{v} v m m m q q q p p p p p p E ′ → \overrightarrow{E'} E ′ v ⃗ \vec{v} v E ⃗ \vec{E} E o o o p p p r ′ ⃗ \vec{r'} r ′ r ⃗ \vec{r} r
我们以 r ′ ⃗ \vec{r'} r ′ r ′ r' r ′ v ⃗ \vec{v} v r r r s ′ = 4 π r ′ 2 s' = 4 \pi {r'}^2 s ′ = 4 π r ′ 2 o o o
在惯性参照系 s s s o o o v ⃗ \vec{v} v x x x v ⃗ \vec{v} v B ⃗ \vec{B} B
很简单的想法是运动电场 E ⃗ \vec{E} E v ⃗ \vec{v} v B ⃗ \vec{B} B v ⃗ \vec{v} v E ⃗ \vec{E} E
B ⃗ = 常数乘以 ( v ⃗ × E ⃗ ) \begin{equation}\nonumber
\vec{B} = \text{常数乘以}\ (\vec{v} \times \vec{E})
\end{equation} B = 常数乘以 ( v × E ) 为了得到运动电场 E ⃗ \vec{E} E
E ′ → = q r ′ ⃗ 4 π ε 0 r ′ 3 \begin{equation}\nonumber
\overrightarrow{E'} = \dfrac{q\ \vec{r'}}{4\pi\ \varepsilon_0\ {r'}^3}
\end{equation} E ′ = 4 π ε 0 r ′ 3 q r ′ 利用洛伦兹正变换【因为电荷 o o o
E ⃗ = q γ 4 π ε 0 ( x − v t ) i ⃗ + y j ⃗ + z k ⃗ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 3 2 \begin{equation}\nonumber
\vec{E} = \dfrac{q\ \gamma}{4\pi\ \varepsilon_0}\ \dfrac{(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}}
\end{equation} E = 4 π ε 0 q γ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 2 3 ( x − v t ) i + y j + z k 所以,
v ⃗ × E ⃗ = q γ 4 π ε 0 v ⃗ × [ ( x − v t ) i ⃗ + y j ⃗ + z k ⃗ ] [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 3 2 \begin{equation}\nonumber
\vec{v} \times \vec{E} = \dfrac{q\ \gamma}{4\pi\ \varepsilon_0}\ \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}}
\end{equation} v × E = 4 π ε 0 q γ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 2 3 v × [( x − v t ) i + y j + z k ] 令真空磁导率为 μ 0 \mu_0 μ 0
B ⃗ = μ 0 q γ 4 π v ⃗ × [ ( x − v t ) i ⃗ + y j ⃗ + z k ⃗ ] [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 3 2 = μ 0 ε 0 q γ 4 π ε 0 v ⃗ × [ ( x − v t ) i ⃗ + y j ⃗ + z k ⃗ ] [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 3 2 = μ 0 ε 0 v ⃗ × E ⃗ \begin{equation}\nonumber
\begin{aligned}
\vec{B} &= \dfrac{\mu_0\ q\ \gamma}{4 \pi} \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \\
&= \dfrac{\mu_0\ \varepsilon_0\ q\ \gamma}{4 \pi\ \varepsilon_0} \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \\
&= \mu_0\ \varepsilon_0\ \vec{v} \times \vec{E}
\end{aligned}
\end{equation} B = 4 π μ 0 q γ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 2 3 v × [( x − v t ) i + y j + z k ] = 4 π ε 0 μ 0 ε 0 q γ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 2 3 v × [( x − v t ) i + y j + z k ] = μ 0 ε 0 v × E 由于
μ 0 ε 0 = 1 c 2 \begin{equation}\nonumber
\mu_0\ \varepsilon_0 = \dfrac{1}{c^2}
\end{equation} μ 0 ε 0 = c 2 1 所以,上式也是可以写成
B ⃗ = 1 c 2 v ⃗ × E ⃗ \vec{B} = \dfrac{1}{c^2}\ \vec{v} \times \vec{E} B = c 2 1 v × E 所以,磁场的定义方程为:
B ⃗ = μ 0 q γ 4 π v ⃗ × [ ( x − v t ) i ⃗ + y j ⃗ + z k ⃗ ] [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 3 2 = μ 0 q γ 4 π v ( − z j ⃗ + y k ⃗ ) [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 3 2 \begin{equation}\nonumber
\begin{aligned}
\vec{B} &= \dfrac{\mu_0\ q\ \gamma}{4 \pi} \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}} \\
&= \dfrac{\mu_0\ q\ \gamma}{4 \pi} \dfrac{v\ (-z \vec{j} + y\ \vec{k})}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}}
\end{aligned}
\end{equation} B = 4 π μ 0 q γ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 2 3 v × [( x − v t ) i + y j + z k ] = 4 π μ 0 q γ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 2 3 v ( − z j + y k ) 上式中,人类以前一直不清楚电荷 q q q q q q
q = − k ′ k 1 Ω 2 d Ω d t \begin{equation}\nonumber
q = -\ k'\ k\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt}
\end{equation} q = − k ′ k Ω 2 1 d t d Ω 可以得到磁场的几何形式定义方程:
B ⃗ = − μ 0 k ′ k 4 π 1 Ω 2 d Ω d t γ v ⃗ × [ ( x − v t ) i ⃗ + y j ⃗ + z k ⃗ ] [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 3 2 \begin{equation}\nonumber
\vec{B} = -\ \dfrac{\mu_0\ k'\ k}{4 \pi}\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt}\ \gamma\ \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}}
\end{equation} B = − 4 π μ 0 k ′ k Ω 2 1 d t d Ω γ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 2 3 v × [( x − v t ) i + y j + z k ] 令 θ \theta θ r ⃗ \vec{r} r v v v B ⃗ \vec{B} B
B ⃗ = − μ 0 k ′ k 4 π 1 Ω 2 d Ω d t v s i n θ γ 2 r 2 ( 1 − β 2 s i n 2 θ ) 3 2 e r ⃗ \begin{equation}\nonumber
\vec{B} = -\ \dfrac{\mu_0\ k'\ k}{4 \pi}\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt}\ \dfrac{v\ sin\theta}{\gamma^2\ r^2\ (1 - \beta^2\ sin^2\theta)^\frac{3}{2}} \vec{e_r}
\end{equation} B = − 4 π μ 0 k ′ k Ω 2 1 d t d Ω γ 2 r 2 ( 1 − β 2 s i n 2 θ ) 2 3 v s in θ e r 式中的 β = v c \beta = \dfrac{v}{c} β = c v c c c v v v v ⃗ \vec{v} v e r ⃗ \vec{e_r} e r r ⃗ \vec{r} r r r r
利用质量和电荷之间的关系 q = k ′ d m d t = − k ′ k 1 Ω 2 d Ω d t q = k'\ \dfrac{dm}{dt} = -\ k'\ k\ \dfrac{1}{\Omega^2}\ \dfrac{d\Omega}{dt} q = k ′ d t d m = − k ′ k Ω 2 1 d t d Ω
B ⃗ = μ 0 k ′ 4 π d m d t γ v ⃗ × [ ( x − v t ) i ⃗ + y j ⃗ + z k ⃗ ] [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 3 2 \begin{equation}\nonumber
\vec{B} = \dfrac{\mu_0\ k'}{4 \pi}\ \dfrac{dm}{dt}\ \gamma\ \dfrac{\vec{v} \times [(x-vt)\ \vec{i} + y\ \vec{j} + z\ \vec{k}]}{[\gamma^2\ (x - vt)^2 + y^2 + z^2]^\frac{3}{2}}
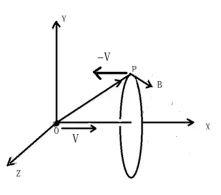
\end{equation} B = 4 π μ 0 k ′ d t d m γ [ γ 2 ( x − v t ) 2 + y 2 + z 2 ] 2 3 v × [( x − v t ) i + y j + z k ] 在下图中,一个相对于我们静止的带正电荷粒子 o o o p p p E ′ → \overrightarrow{E'} E ′ o o o v ⃗ \vec{v} v x x x B ⃗ \vec{B} B B ⃗ \vec{B} B v ⃗ \vec{v} v
磁场 B ⃗ \vec{B} B E ⃗ \vec{E} E v ⃗ \vec{v} v
B ⃗ = 1 c 2 v ⃗ × E ⃗ \begin{equation}\nonumber
\vec{B} = \dfrac{1}{c^2}\ \vec{v} \times \vec{E}
\end{equation} B = c 2 1 v × E 按照矢量叉乘和斯托克斯定理排列顺序的习惯,y y y z z z x x x z z z x x x y y y x x x y y y z z z
B x → = 0 ⃗ B y → = − 1 c 2 v ⃗ × E z → B z → = 1 c 2 v ⃗ × E y → \begin{align}
\overrightarrow{B_x} &= \vec{0} \nonumber \\
\overrightarrow{B_y} &= -\ \dfrac{1}{c^2}\ \vec{v} \times \overrightarrow{E_z} \nonumber \\
\overrightarrow{B_z} &= \dfrac{1}{c^2}\ \vec{v} \times \overrightarrow{E_y} \nonumber
\end{align} B x B y B z = 0 = − c 2 1 v × E z = c 2 1 v × E y 其中 v ⃗ \vec{v} v o o o x x x
按照统一场论的看法,物体粒子静止时候周围空间点的运动速度是矢量光速 c ′ ⃗ \vec{c'} c ′ v ⃗ \vec{v} v c ⃗ − v ⃗ \vec{c} - \vec{v} c − v
o o o p p p c ′ ⃗ \vec{c'} c ′ o o o v ⃗ \vec{v} v x x x p p p E ⃗ \vec{E} E − v ⃗ -\vec{v} − v o o o v ⃗ \vec{v} v
当我们把考察点放在 p p p o o o p p p
B x → = 0 ⃗ B y → = 1 c 2 v ⃗ × E z → B z → = − 1 c 2 v ⃗ × E y → \begin{align}
\overrightarrow{B_x} &= \vec{0} \nonumber \\
\overrightarrow{B_y} &= \dfrac{1}{c^2}\ \vec{v} \times \overrightarrow{E_z} \nonumber \\
\overrightarrow{B_z} &= -\ \dfrac{1}{c^2}\ \vec{v} \times \overrightarrow{E_y} \nonumber
\end{align} B x B y B z = 0 = c 2 1 v × E z = − c 2 1 v × E y 当我们考察空间点 p p p
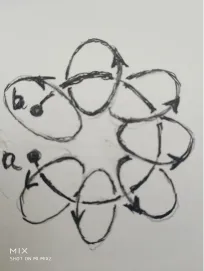
在下图中,当电荷 o o o a a a b b b S S S N N N
从磁场这种几何形式来看,自然界不存在有磁单极子的。
Learn