The experiment of changing electromagnetic fields generating gravitational fields at low voltages

Author

Section titled Author

Xiangqian Zhang

• WeChat: 18714815159

Foreword

Section titled Foreword

In 1831, British scientist Michael Faraday conducted an experiment and discovered the phenomenon of electromagnetic induction, thus achieving the conversion between electricity and magnetism. From then on, humankind entered the era of electrical civilization.

Humanity has been continuously exploring the fundamental laws of electricity and magnetism. Albert Einstein dedicated over 40 years of his life trying to unify electromagnetism with gravity, but unfortunately, he did not succeed.

The unified field theory that I brought forth for the first time in human history pointed out the mathematical relationship that electromagnetic fields and gravitational fields satisfy.

On November 2, 2023, I conducted an experiment and discovered the gravitational field effect for the first time. Since then, I have persisted in conducting further experiments. However, I have found that it requires voltages of tens of thousands to observe the gravitational field effect.

Due to the presence of high voltage, there are accompanying effects such as the electrostatic motor effect, polarization effect, and ion wind effect, making it difficult to distinguish them from the gravitational field effect, thus reducing the persuasiveness of the experiments.

Recently, Mr. Xu from Anhui Develop Amorphous Equipment Co., Ltd. has been collaborating with me on experiments. Under my theoretical guidance, they have discovered that changing electromagnetic field can generate gravitational field effects even at low voltages.

They have observed significant gravitational field effects at low voltages ranging from 12 volts to 160 volts. This discovery is considered the most significant scientific breakthroughs since Faraday’s discovery of electromagnetic induction in 1831.

This indicates that the era of field civilization, replacing the era of electrical civilization, has arrived.

Mr. Xu has already submitted an application for this experiment to the National Patent Office. A few days ago, they received the acceptance letter from the National Patent Office.

Today, I am publishing the detailed experimental method, and netizens, universities, and research institutes with experimental capabilities can replicate this experiment. The experiment is simple and the cost does not exceed ten thousand yuan.

Experimental Method

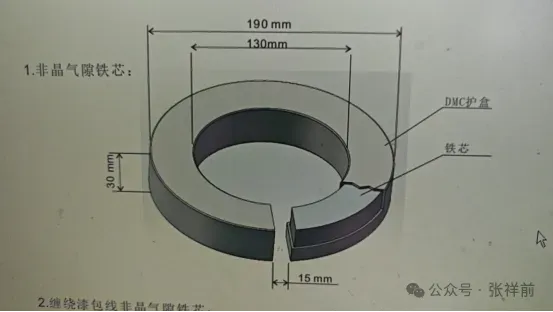
Section titled Experimental Method

Selection of Soft Magnetic Toroidal Iron Core with Amorphous Material [Conventional silicon steel sheets with a thickness of 0.2 to 0.5 millimeters can also be used]. The amorphous material has a saturation magnetic induction intensity (Bs) of 1.25 Tesla (T) and a permeability greater than or equal to 100,000. The inner diameter of the iron core is 130 mm, the outer diameter is 190 mm, and the thickness is 30 mm.

A 15 mm long incision is made on the toroidal core, creating a 15 mm long air gap. A 2 mm diameter enameled copper wire is wound around the toroidal core to form an excitation winding with 400 turns.

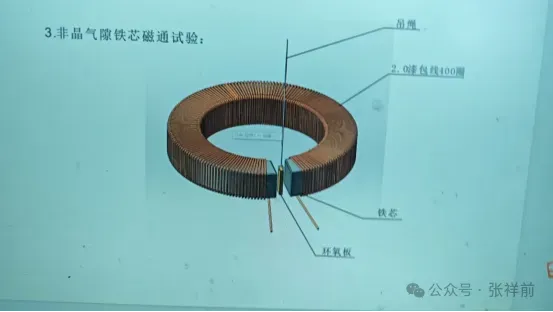
During the experiment, when the coil is energized with an alternating current of I = 30 A, frequency f = 50 Hz, and voltage V = 80 V.

An alternating magnetic flux is generated at the air gap of the iron core. The peak magnetic field intensity at the air gap is measured to be approximately 0.1 to 0.3 Tesla (T).

Various test materials suspended by fine wires at the air gap include:

1. epoxy resin board (strong insulating material);
2. ceramics
3. plastic
4. stainless steel
5. green leaves
6. fresh pork
7. polyethylene
8. aluminum
9. rubber
10. paper
11. glass
12. copper
13. organic glass…… and other materials

After energizing the coil, it is observed that all objects can undergo motion, and the direction of motion is perpendicular to the magnetic field lines obviously.

Along a perpendicular cross-section of the magnetic field lines at the air gap, if any of these test materials are placed at the air gap, they will move towards the center point of the cross-section in the direction perpendicular to the magnetic field lines.

This type of motion is similar to the motion induced by the gravitational field on the Earth’s surface, leading us to believe that the changing electromagnetic field is generating a gravitational field.

We have also conducted experiments using direct current ranging from 12V to 80V and current ranging from 30A to 130A, and the results are similar to those obtained with alternating current. The DC power supply can be provided by a battery or an AC to DC power supply.

Theoretical derivation

Section titled Theoretical derivation

1. Fundamental Assumptions

Section titled 1. Fundamental Assumptions

Animations

These demo animations were [email protected] created and added for the reader to better understand the concepts.

It is worth mentioning that: The animations are just to help readers understand the concepts. If there is a discrepancy between the animation and the textual description, please always refer to the text.

If you find a error in it, please report the error here, thank you!

In the universe any object’s surrounding space always spreads outward in all directions in a cylindrical spiral motion at the velocity of light denoted as the vector velocity $\vec{C^\prime}$ (capital letters denote vectors).

In the framework of Unified Field Theory, the straight linear motion component of the cylindrical spiral motion represents the electric field, the rotational motion component represents the magnetic field, and the acceleration directed towards the central axis in the rotational motion represents the gravitational field. These three fields are mutually perpendicular to each other.

Electric Field

Section titled Electric Field

When space is in motion, it generates an electric field in the direction of its movement. When space comes to a stop, the electric field disappears.

Magnetic Field

Section titled Magnetic Field

When space is in motion, it generates a magnetic field in the direction tangent to its rotation. When space stops rotating, the magnetic field disappears.

Gravitational Field

Section titled Gravitational Field

When space is in a spiral motion, it exhibits an acceleration towards the center, which is referred to as the gravitational field. When space stops its spiral motion, the gravitational field disappears.

Even stationary objects have a magnetic field around them. However, the number of magnetic field lines entering a surface is equal to the number of magnetic field lines exiting that surface, effectively canceling each other out and not exhibiting any noticeable effects externally.

The above assumptions mentioned the motion of space itself.

To describe the motion of space itself, we divide space into many small units called space points. By describing the motion of these space points, we can describe the motion of space itself.

The above assumptions mentioned the vectorial light speed.

The text argues that the speed of light can be extended to a vector quantity, where the direction of vectorial light speed can change. The magnitude of this vectorial speed is the scalar speed of light, denoted by the lowercase letter $c$, which remains constant.

When the particle at point $o$ is stationary relative to an observer, a surrounding space point, denoted by $p$, moves outward in a radial motion with a vectorial speed $\vec{C^\prime}$. When the point $o$ moves with a velocity $\vec{V}$ relative to the observer, the velocity of point $p$ relative to the observer is represented by the vectorial speed $\vec{C}$.

$\vec{C^\prime}$ and $\vec{C}$ have the same magnitude but different directions. Does the relationship between $\vec{C^\prime}$ and $\vec{C}$ onform to the Lorentz transformation of relativity?

According to the Lorentz velocity transformation, the relationship between the three components $\vec{C}x^{\prime}, \vec{C}y^{\prime}, \vec{C}z^{\prime}$ of $\vec{C^\prime}$ and the three components $\vec{C}x, \vec{C}y, \vec{C}z$ of $\vec{C}$ is given by:

$$\vec{C}x^{\prime} = \dfrac{(\vec{C}x - v)}{[1 - (\vec{C}x \dfrac{v}{c²})]}$$ $$\vec{C}y^{\prime} = \dfrac{[\vec{C}y \sqrt{(1 - \dfrac{v²}{c²})}]}{[1 - (\vec{C}x \dfrac{v}{c²})]}$$ $$\vec{C}z^{\prime} = \dfrac{[\vec{C}z \sqrt{(1 - \dfrac{v²}{c²})}]}{[1 - (\vec{C}x \dfrac{v}{c²})]}$$

From the above, it can be derived:

$$(\vec{C}x^{\prime})^2 + (\vec{C}y^{\prime})^2 + (\vec{C}y^{\prime})^2$$ $$= \dfrac{[(\vec{C}x - v)²+ \vec{C}y²(1 - \dfrac{v²}{c²}) + \vec{C}z²(1 - \dfrac{v²}{c²})]}{[1 - (\vec{C}x \dfrac{v}{c²})]²}$$ $$= c²c² \dfrac{[\vec{C}x²+ \vec{C}y²+ \vec{C}z²-2 \vec{C}x v+ v²-(c²-\vec{C}x²)\dfrac{v²}{c²}]}{(c²-\vec{C}x v)²}$$ $$= c²c²\dfrac{[c²-2 \vec{C}x v+ v²-(c²-\vec{C}x²)\dfrac{v²}{c²}]}{(c²-\vec{C}x v)²}$$ $$= c² \dfrac{[c²c²-2 c²\vec{C}x v+ \vec{C}x²v²]}{(c²-\vec{C}x v)²}$$ $$= c²$$

From this, it can be derived that the vector velocities $\vec{C}$ and $\vec{C^{\prime}}$ satisfy the following relationship:

$$\vec{C^\prime}·\vec{C^\prime} = \vec{C}·\vec{C} = c^2$$

$\vec{C}$ and $\vec{C^\prime}$ have different directions, but their magnitudes are equal.

When point $o$ is moving with velocity $\vec{V}$ relative to the observer, let point $p$ have a velocity $\vec{U}$ relative to point $o$. Since $\vec{C}$ is the composition of $\vec{U}$ and $\vec{V}$, we have $\vec{C}$ = $\vec{U}$ + $\vec{V}$,

Therefore:

$\vec{U}$ = $\vec{C}$ - $\vec{V}$

2. Understanding the gravitational field

Section titled 2. Understanding the gravitational field

We stand on Earth and drop a stone casually, the stone falls freely towards the center of the Earth with an acceleration.

If there were no stone, the space where the stone would be still falls towards the center of the Earth in the same manner. This is the essence of a gravitational field.

The essence of a gravitational field is the acceleration of the surrounding space towards the center of mass of an object.

A gravitational field has two important properties:

The position vector from an object to a point in the gravitational field (referred to as a field point or observation point) is directed in the opposite direction of the gravitational field.

A gravitational field can exert an accelerating effect on objects made of any material.

3. Understanding Magnetic Fields

Section titled 3. Understanding Magnetic Fields

Humans have discovered that when charged particles move in a straight line at a constant velocity relative to an observer, it causes changes in the electric field in the direction perpendicular to the motion. This changing part of the electric field can be considered as a magnetic field, which is generated by the changing electric field resulting from the change in velocity.

In the diagram below, a positively charged particle at point $o$, which is stationary relative to us, creates an electrostatic field $\vec{E^\prime}$ at point $p$ in the surrounding space. When the particle at point $o$ moves in a straight line at a constant velocity $\vec{V}$ along the positive $x$-axis relative to the observer, it can generate a magnetic field $\vec{B}$.

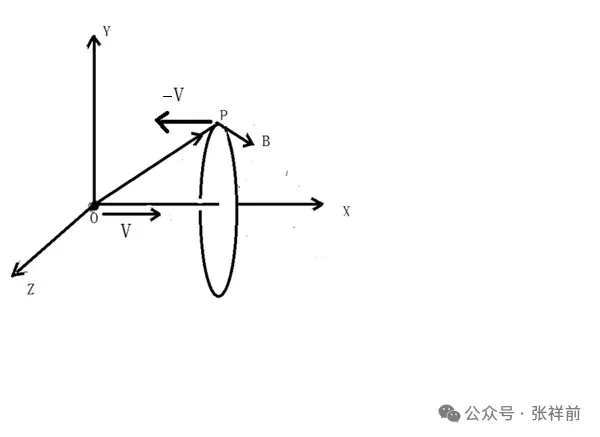
The essence of this magnetic field is that space rotates around the vector velocity $\vec{V}$ as its central axis. The rotation of $\vec{B}$ is such that it satisfies the right-hand rule relationship with $\vec{V}$, forming a right-handed helix.

$$\vec{B} = \vec{V} · \dfrac{\vec{E}}{c^2}$$

According to the convention of the order of arrangement of vector cross product and Stokes’ theorem, when the vector $y$ is crossed with $z$, it forms a vector surface element in the $x$ direction. When $z$ is crossed with $x$, it forms a vector surface element along the $y$ direction. When $x$ is crossed with $y$, it forms a vector surface element along the $z$ direction. The three components satisfy the following right-hand screw rule relationship:

$$\vec{B_x} = 0$$ $$\vec{B_y} = -\vec{V} · \dfrac{\vec{E_z}}{c^2}$$ $$\vec{B_z} = \vec{V} · \dfrac{\vec{E_y}}{c^2}$$

Point $o$ is a positive charge, where $\vec{E_z}$ represents the component of the electric field generated by point $o$ along the $z$-axis, and $\vec{E_y}$ represents the component along the $y$-axis.

The positive electric field generated by point $o$ points from point $o$ towards point $p$.

Based on the previous assumption, when point $o$ moves with a velocity $\vec{V}$ along the positive $x$-axis, the space point $p$ has an opposite velocity $- \vec{V}$.

If we move the observation point away from point $o$ and instead place it at point $p$ in space, then the aforementioned right-hand screw relationship would be changed to a left-hand screw relationship:

$$\vec{B_x} = 0$$ $$\vec{B_y} = \vec{V} · \dfrac{\vec{E_z}}{c^2}$$ $$\vec{B_z} = - \vec{V} · \dfrac{\vec{E_y}}{c^2}$$

When we analyze the motion of a certain point $p$ in space, using this component formula is more direct and convenient.

4. A time-varying magnetic field generates an electric field and a gravitational field

Section titled 4. A time-varying magnetic field generates an electric field and a gravitational field

In Unified Field Theory, the curl of the gravitational field $\vec{A}$ and the uniform magnetic field $\vec{B}$ satisfy the following relationship:

$$\vec{\nabla} · \vec{A} = \dfrac{1}{f} \vec{B}$$

The constant $f$ represents a constant factor in the equation. This equation represents the fundamental relationship between the magnetic field and the gravitational field. It tells us that the magnetic field produced when a charge moves in a straight-line motion at a constant velocity can be expressed in terms of the curl of the gravitational field.

The concept of the magnetic vector potential introduced in electromagnetism and quantum mechanics is not a meaningless concept, but rather it represents the vortex gravitational field. This equation may be the final explanation for the Aharonov-Bohm effect in quantum mechanics.

By taking the dot product of both sides of the equation with a vector surface element (which can be considered as a small area on a Gaussian spherical surface $s = 4πr²$ surrounding the charged particle at point $o$, with its outward normal direction), and then utilizing the Stokes’ Theorem in field theory, we can obtain an integral equation that describes the relationship between the magnetic field and the gravitational field:

$$\oint \vec{A} ·d\vec{l} = \dfrac{1}{f} \oiint \vec{B} · d \vec{S}$$

This gravitational field, with magnetic field lines as its axis, exhibits a right-handed spiral distribution around in space.

Next, let’s consider the variations of the magnetic field $\vec{B}$.

Consider a positive point charge at point $o$, starting from the origin of Cartesian coordinates at time $t = 0$, moving along the positive $x$-axis with a constant velocity (its magnitude is $v$), relative to the observer.

In the reference frame of the $s$ system, (the $s^\prime$ system moves with a constant velocity along the positive $x$-axis relative to the s system), the point charge $o$ generates an electric field $\vec{E}$ and a magnetic field $\vec{B}$ around the space point $p$, adjusting to the right-handed spiral, as shown in the diagram below.

If we consider the space point $p$ as the observation point instead of the charge point $o$, the velocities of the point charge $o$ and the point $p$ are in opposite directions ($\vec{V}$ and $- \vec{V}$, respectively). Therefore, in this case, the moving electric field $\vec{E}$ and the uniform magnetic field $\vec{B}$ satisfy the left-handed spiral relationship as described by the equation:

$$\vec{B} = - \dfrac{1}{c^2} \vec{v} · \vec{E}$$

The components can be expressed as:

$$\vec{B_x} = 0$$ $$\vec{B_y} = \dfrac{v}{c^2} · \vec{E_z}$$ $$\vec{B_z} = - \dfrac{v}{c^2} · \vec{E_y}$$

Taking the derivative of the above $\vec{B} = - \dfrac{1}{c^2} \vec{v} · \vec{E}$ equation with respect to time $t$, we have:

$$\dfrac{d \vec{B}}{dt} = - \dfrac{1}{c^2} \dfrac{d\vec{v}}{dt} · \vec{E} - \dfrac{1}{c^2} \vec{v} · \dfrac{d\vec{E}}{dt}$$

If we can prove that the second term on the right side of the equation represents the electric field generated by the changing magnetic field (also known as the vortex electric field), which corresponds to Faraday’s electromagnetic induction principle, then the additional first term should represent the gravitational field generated by the changing magnetic field.

Because $\dfrac{dv}{dt}$ represents the acceleration of the space point $p$, according to the principles of Unified Field Theory, the acceleration of space itself is equivalent to the gravitational field.

Let’s start by proving that the second term on the right side of the equation represents Faraday’s electromagnetic induction principle.

The three components are as follows (replacing the differential symbol $d$ with the partial differential symbol $\partial$):

$$\dfrac{\partial \vec{B_x}}{\partial t} = 0$$ $$\dfrac{\partial \vec{B_y}}{\partial t} = \dfrac{v}{c^2} \dfrac{\partial \vec{E_z}}{\partial t}$$ $$\dfrac{\partial \vec{B_z}}{\partial t} = - \dfrac{v}{c^2} \dfrac{\partial \vec{E_y}}{\partial t}$$

The curl of the electrostatic field is zero

$$\dfrac{\partial \vec{E_x^{\prime}}}{\partial z{^\prime}} - \dfrac{\partial \vec{E_z^{\prime}}}{\partial x{^\prime}} = 0$$

and the Lorentz transformation

$$\vec{E_x} = \vec{E_x^{\prime}}, \partial z^{\prime} = \partial z, \vec{E_z^{\prime}} = \dfrac{1}{\gamma} \vec{E_z},$$ $$\dfrac{\partial}{ \partial x{^\prime}} = \dfrac{1}{\gamma} \dfrac{\partial}{\partial x}, \gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}$$

resulting in:

$$\dfrac{\partial \vec{E_x}}{\partial z} - \dfrac{1}{\gamma^2} \dfrac{\partial \vec{E_z}}{\partial x} = 0$$

So,

$$\dfrac{\partial \vec{E_x}}{\partial z} - \left( 1 - \dfrac{v^2}{c^2} \right) \dfrac{\partial \vec{E_z}}{\partial x} = 0$$

By the definition of velocity,

$$\dfrac{\partial \vec{E_x}}{\partial z} - \dfrac{\partial \vec{E_z}}{\partial x} = - \dfrac{v}{c^2} \dfrac{\partial \vec{E_z}}{\partial t}$$

Similar operations can be performed to obtain:

$$\dfrac{\partial \vec{E_y}}{\partial x} - \dfrac{\partial \vec{E_x}}{\partial y} = \dfrac{v}{c^2} \dfrac{\partial \vec{E_y}}{\partial t}$$

By comparing these two equations with the three components mentioned above, we can obtain:

$$\dfrac{\partial \vec{E_z}}{\partial y} - \dfrac{\partial \vec{E_y}}{\partial z} = 0$$ $$\dfrac{\partial \vec{E_x}}{\partial z} - \dfrac{\partial \vec{E_z}}{\partial x} = - \dfrac{\partial \vec{B_y}}{\partial t}$$ $$\dfrac{\partial \vec{E_y}}{\partial x} - \dfrac{\partial \vec{E_x}}{\partial y} = - \dfrac{\partial \vec{B_z}}{\partial t}$$

Combining the above three equations yields the Faraday’s electromagnetic induction equation:

$$\vec{\nabla} · \vec{E} = - \dfrac{\partial \vec{B}}{\partial t}$$

Next, let’s analyze the equation that describes the gravitational field generated by a changing magnetic field.

This equation can be understood as follows: when the magnetic field $\vec{B}$ changes with time $t$, it can generate an electric field $\vec{E}$ and a gravitational field $\vec{A}$. Furthermore, at a certain point in space, $\vec{B}$, $\vec{A}$ and $\vec{E}$ are mutually perpendicular to each other.

The experiments conducted above confirm that all objects move in the direction perpendicular to the magnetic field lines at the air gap.