Skip to content
Unified Field Theory

二十三、引力场和质量的定义方程

在统一场论中，物体 oo 点的质量 mm，表示了 oo 点周围 4π4\pi 立体角度内以光速、以圆柱状螺旋式发散运动空间位移 r⃗\vec{r} 的条数。

oo 点在周围产生的引力场 A⃗\vec{A} ，表示了穿过包围 oo 点的高斯球面 ss 上，以光速发散运动的空间位移的条数。

点击展开注解：什么是“高斯球面”？

引力场的定义方程

Section titled 引力场的定义方程

设想有一个质点 oo 相对于我们观测者静止，周围空间中任意一个空间点 pp，在零时刻以矢量光速度 c⃗\vec{c} 从 oo 点出发，以圆柱状螺旋式沿某一个方向运动，经历了时间 tt，在 t′t' 时刻到达 pp 后来所在的位置。

我们让点 oo 处于直角坐标系 xyzxyz 的原点，由 oo 点指向 pp 点的矢径 r⃗\vec{r} 由前面的时空同一化方程 r⃗(t)=c⃗t=xi⃗+yj⃗+zk⃗\vec{r}(t) = \vec{c}t = x\vec{i} + y\vec{j} + z\vec{k} 给出，r⃗\vec{r} 是空间位置 x,y,zx, y, z 和时间 tt 的函数，随 x,y,z,tx, y, z, t 的变化而变化，记为：

r⃗=r⃗(x,y,z,t)\begin{equation}\nonumber \vec{r} = \vec{r}(x, y, z, t) \end{equation}
点击展开注解：关于此处将 r⃗\vec{r} 写成了一个关于 x,y,z,tx, y, z, t 的四元函数

注意，pp 点在空间中走过的轨迹是圆柱状螺旋式，我们也可以认为是矢径 r⃗\vec{r} 的一个端点 oo 不动，另一个端点 pp 运动变化，使得 r⃗\vec{r} 在空间中划过一条圆柱状螺旋式轨迹。

我们以 r⃗=c⃗t\vec{r} = \vec{c}t 中 r⃗\vec{r} 的标量长度 rr 为半径，作高斯球面 s=4πr2s = 4 \pi r^2【在普遍情况下，高斯球面可以不是一个正球面，但是，球面是连续的、不能有破洞】包围质点 oo。

我们把高斯球面 s=4πr2s = 4 \pi r^2 均匀的分割成许多小块，我们选择 pp 点所在的一小块矢量面元 ΔS⃗\Delta\vec{S}【 ΔS⃗\Delta\vec{S} 方向我们用 N⃗\vec{N} 来表示，其数量为曲面 ΔS\Delta{S} 】，我们考察发现 ΔS\Delta{S} 上有 Δn\Delta{n} 条类似于 pp 的空间点的位移矢量 r⃗\vec{r} 垂直的穿过。

注意：高斯球面 ss 的半径也可以不等于 r⃗\vec{r} 的标量长度，我们设定是相等的，好处是使考察点 pp 恰巧落在高斯球面 ss 上。

这样，oo 点在空间点 pp 处产生的引力场 A⃗\vec{A}【数量为 AA】:

A=常数乘以ΔnΔS\begin{equation}\nonumber A = \text{常数乘以} \dfrac{\Delta{n}}{\Delta{S}} \end{equation}
点击展开注解：与“电场强度”的类比

上式给出的引力场定义简单明了，但过于粗糙，不能把引力场矢量性质表现出来，也没有把以矢量光速运动的空间位移 r⃗\vec{r} 带进式子中去。

为了达到以上目的，我们主要考察 pp 点周围情况。

pp 点的矢量位移 r⃗=c⃗t\vec{r} = \vec{c}t 垂直的穿过 ΔS⃗\Delta\vec{S} ，普遍情况下，矢量位移 r⃗=c⃗t\vec{r} = \vec{c}t 可以不是垂直的穿过 ΔS⃗\Delta\vec{S}，可以和矢量面元 ΔS⃗\Delta\vec{S} 的法方向 N⃗\vec{N} 有一个夹角 θ\theta。

在 oo 点相对于我们观察者静止，oo 点周围空间的运动是均匀的，没有那个方向是特殊的，而且，我们使用的高斯球面是一个正圆球面，在这些条件限制下，矢量 r⃗=c⃗t\vec{r} = \vec{c}t 才是垂直穿过矢量面元 ΔS⃗\Delta \vec{S}

这样，oo 点在周围空间 pp 点处产生的引力场 A⃗\vec{A}【矢量形式】可以写为：

A⃗=−G k Δn r⃗ΔS r\begin{equation}\nonumber \vec{A} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} \end{equation}

式中 GG 是万有引力常数，kk 是比例常数。注意，引力场 A⃗\vec{A} 和由 oo 点指向空间点 pp 的位矢 r⃗\vec{r} 方向相反。

设想 oo 点周围有 nn 条类似于 r⃗\vec{r} 的空间位移矢量，以 oo 点为中心，呈辐射状分布，但是，任意两条的方向都不一样。

而 nn 乘以 r⃗\vec{r} 即 nr⃗n\vec{r} 的物理意义表示 nn 条空间位移的方向都是一样的，叠加在一起。

所以，当以上的 r⃗\vec{r} 为矢量，只有 Δn=1\Delta{n}=1 的情况下，才具有物理意义。但是，我们要注意 nn 乘以 rr【rr 是 r⃗\vec{r} 的数量】中，当 nn 是大于1的整数仍然具有物理意义。

所以有式：

A⃗=−G k Δn r⃗ΔS r=−G k r⃗ΔS r\begin{equation}\nonumber \vec{A} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} = - \dfrac{G\ k\ \vec{r}}{\Delta{S}\ r} \end{equation}
点击展开疑问

上式中为什么用 r⃗\vec{r} 的单位矢量 r⃗c\dfrac{\vec{r}}{c}，而不是直接用矢量 r⃗\vec{r} ？

是因为我们在高斯球面 ss 上只能考察矢量 r⃗\vec{r} 的方向和条数，而不能考察矢量 r⃗\vec{r} 的长度，所以 Δn r⃗ΔS\dfrac{\Delta{n}\ \vec{r}}{\Delta{S}} 这个式子其实是没有物理意义的。

如果 r⃗\vec{r} 不完全是垂直穿过矢量面元 ΔS⃗\Delta\vec{S}【数量为 ΔS\Delta{S} 】，和矢量面元的法方向 N⃗\vec{N} 具有一个角度 θ\theta，当空间点的位移 r⃗\vec{r} 的条数 nn 设定为1的时候，以上方程也可以用矢量点乘公式来表示。

A⃗⋅ΔS⃗=−A ΔS cosθ=−G k Δn\begin{equation}\nonumber \vec{A} \cdot \Delta \vec{S} = - A\ \Delta S\ cos\theta = -G\ k\ \Delta n \end{equation}
点击展开公式修正：最后一个式子似乎少乘了一个 cosθcos \theta

上式中 AA 是引力场 A⃗\vec{A} 的数量。

引力场 A⃗\vec{A} 是由大小和方向余弦两个量决定的。

大小是指光速运动空间位移 r⃗\vec{r} 在高斯球面 ss 上分布的密度（1ΔS\dfrac{1}{\Delta S}）。

1ΔS\dfrac{1}{\Delta S} 或者 ΔnΔS\dfrac{\Delta n}{\Delta S} 表示了含两个自变量的函数，随 Δn\Delta n 和 ΔS\Delta S 变化而变化。

方向余弦是 ΔS⃗\Delta \vec{S} 的法方向 N⃗\vec{N} 和 r⃗\vec{r} 的夹角 θ\theta 的余弦，也就是 cosθcos \theta。

方向余弦 cosθcos \theta 是只含一个自变量的函数，这个函数随 θ\theta 变化而变化。

式

A=常数乘以ΔnΔS\begin{equation}\nonumber A = \text{常数乘以} \dfrac{\Delta{n}}{\Delta{S}} \end{equation}

和

A⃗=−G k Δn r⃗ΔS r\begin{equation}\nonumber \vec{A} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} \end{equation}

这两个式子的物理意义告诉我们：

高斯球面 s=4πr2s = 4 \pi r^2 其中一小块矢量面元 ΔS⃗\Delta\vec{S} 上，垂直穿过空间矢量位移 r⃗\vec{r}【 r⃗=c⃗t\vec{r} = \vec{c}t 】的密度反映了该处的引力场强度。

我们将式

A⃗=−G k Δn r⃗ΔS r\begin{equation}\nonumber \vec{A} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Delta{S}\ r} \end{equation}

中的 ΔS\Delta S 用立体角 Ω\Omega 和高斯球面的半径 rr 来表示，也就是 ΔS=Ω r2\Delta S = \Omega\ r^2

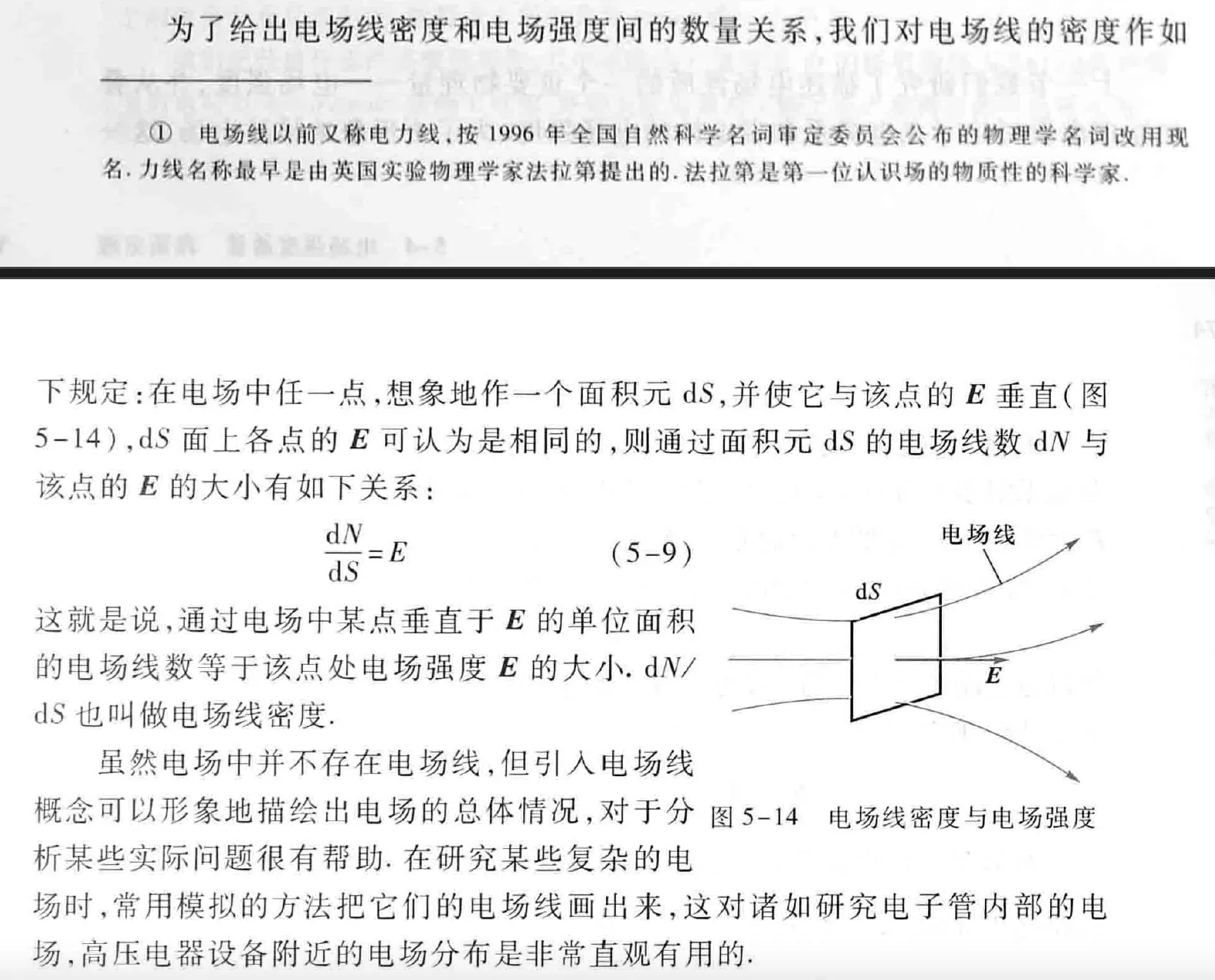
A⃗=−G k Δn r⃗Ω r2 r=−G k Δn r⃗Ω r3\begin{equation}\nonumber \vec{A} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^2\ r} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^3} \end{equation}

上图中，我们将高斯球面中的一小块矢量面元 ΔS\Delta S 用 dSdS 表示。则：

dS=r dθ r sinθ dφ=r2 dθ sinθ dφ=r2 dΩ\begin{equation}\nonumber dS = r\ d\theta\ r\ sin\theta\ d\varphi = r^2\ d\theta\ sin\theta\ d\varphi = r^2\ d\Omega \end{equation}

质量的定义方程

Section titled 质量的定义方程

质量的本质是什么？质量和引力场是什么关系？

由于质量的概念起源于牛顿力学，我们把以上统一场论引力场几何形式的定义方程

A⃗=−G k Δn r⃗Ω r3\begin{equation}\nonumber \vec{A} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^3} \end{equation}

和牛顿力学引力场方程 A⃗=−G m r⃗r3\vec{A} = -\dfrac{G\ m\ \vec{r}}{r^3} 相比较，可以得出物体 oo 点的质量定义方程应该是:

m=k ΔnΩ\begin{equation}\nonumber m = \dfrac{k\ \Delta n}{\Omega} \end{equation}

微分式为：

m=k dndΩ\begin{equation}\nonumber m = \dfrac{k\ dn}{d\Omega} \end{equation}

上式 kk 是常数。由于空间可以无限分割，所以，以上的 nn 的微分，也就是 dndn 是有意义的。

对上式右边环绕积分，积分区域在 00 和 4π4 \pi 之间，则：

m=k ∯dn∯dΩ=k n4π\begin{equation}\nonumber m = k\ \dfrac{\oiint dn}{\oiint d\Omega} = k\ \dfrac{n}{4\pi} \end{equation}

上式的物理意义是：

oo 点的质量 mm 表示周围立体角 4π4\pi 内分布有 nn 条空间位移矢量 r⃗=c⃗t\vec{r} = \vec{c}t

以上

m=k dndΩ\begin{equation}\nonumber m = \dfrac{k\ dn}{d\Omega} \end{equation}

是质量的几何形式的微分定义方程。

在很多种情况下，我们将 nn 设定为1，可以得到质量的简化定义方程：

m=kΩ\begin{equation}\nonumber m = \dfrac{k}{\Omega} \end{equation}
点击展开注解：关于上式中 Ω\Omega 含义的说明

我们一旦知道了质量的本质，就可以对牛顿力学中的引力场方程 A⃗=−G m r⃗r3\vec{A} = -\dfrac{G\ m\ \vec{r}}{r^3} 做出解释。

按照牛顿力学，我们以地球【用 oo 点表示，我们观察者站在地球上】为例，地球上空一个卫星【用 pp 点表示】，由 oo 点指向 pp 点的位置矢量【间称位矢】用 r⃗\vec{r}【数量为rr】表示。

则 oo 点在 pp 点处产生的引力场 A⃗=−G m r⃗r3\vec{A} = -\dfrac{G\ m\ \vec{r}}{r^3}， 表示在以半径为 rr 的高斯球面 s=4πr2s = 4 \pi r^2 上，分割了一小块矢量面元 ΔS⃗\Delta\vec{S}，ΔS⃗\Delta\vec{S} 上穿过了 11 条矢量 r⃗\vec{r} ，并且， r⃗\vec{r} 和 A⃗\vec{A} 方向相反。

ΔS⃗\Delta \vec{S} 的数量 ΔS\Delta{S} 的倒数反映了引力场的大小，ΔS⃗\Delta \vec{S} 的反方向就是引力场的方向。

我们需要注意的是，统一场论的引力场方程，反映了某一个瞬间，或者是某一个时刻的情况。

对统一场论的静止引力场

A⃗=−G k Δn r⃗Ω r3\begin{equation}\nonumber \vec{A} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^3} \end{equation}

求旋度，在 Δn\Delta n 和 Ω\Omega 是常数【也就是质量为常数】的情况下，仅 r⃗r3\dfrac{\vec{r}}{r^3} 是变量，结果为零：

∇⃗×A⃗=0⃗\begin{equation}\nonumber \vec{\nabla} \times \vec{A} = \vec{0} \end{equation}
点击展开注解：关于“旋度”

对静止引力场

A⃗=−G k Δn r⃗Ω r3\begin{equation}\nonumber \vec{A} = - \dfrac{G\ k\ \Delta{n}\ \vec{r}}{\Omega\ r^3} \end{equation}

求散度，在（ m=k ΔnΩm = \dfrac{k\ \Delta n}{\Omega} ）是常数的情况下，仅 r⃗r3\dfrac{\vec{r}}{r^3} 是变量，结果也为零：

∇⃗⋅A⃗=0\begin{equation}\nonumber \vec{\nabla} \cdot \vec{A} = 0 \end{equation}
点击展开注解：关于“散度”

但在 rr 趋近于零【也可以说空间点 pp 无限趋近于 oo 点】，且 oo 点可以看成一个无限小的球体的情况下，式子出现了 00\dfrac{0}{0} 的情况，利用狄拉克 δ\delta 函数，可以得到：

∇⃗⋅A⃗=4π G u\begin{equation}\nonumber \vec{\nabla} \cdot \vec{A} = 4 \pi\ G\ u \end{equation}

GG 是万有引力常数，u=mΔxΔyΔzu = \dfrac{m}{\Delta x \Delta y \Delta z} 是物体 oo 点的密度。

统一场论给出的引力场定义方程的旋度和散度，和牛顿力学给出的引力场的散度、旋度是一致的。

点击展开注解：为什么是一致的？

从质量定义方程导出相对论质速关系

Section titled 从质量定义方程导出相对论质速关系

相对论用动量守恒和相对论速度变换公式，可以导出相对论质速关系——质量随物体运动速度增大而增大。

相对论又用质速关系推导出相对论质能方程，所以，质速关系很重要。

下面我们用质量的定义方程直接导出质速关系。

设想一个质量为 m′m' 的质点 oo ，一直静止在 s′s' 系的坐标原点 o′o' 上。

ss 系相对于 s′s' 系以匀速度 v⃗\vec{v}【标量为 vv 】沿 xx 轴正方向运动，并且 ss 系的 xx 轴和 s′s' 系的 x′x' 轴相互重合。

在 ss 系里的观察者看来 oo 点的质量为 mm，我们用以上的质量几何定义方程 m∯dΩ=k ∯dnm \oiint d\Omega = k\ \oiint dn 来求出 v⃗\vec{v} 和 mm、m′m' 之间满足的数学关系。

当 oo 点运动的时候，我们应该合理的认为，不会引起空间点矢量位移 r⃗\vec{r} 的条数 nn 的变化，只是有可能引起立体角度 Ω\Omega 的变化。所以，我们只要求出运动速度 v⃗\vec{v} 和 Ω\Omega 之间满足的关系，也就是 Ω\Omega 的相对论变换，就可以求出 m′m' 和 mm 之间的关系。

立体角 Ω\Omega 的定义为：

在以 oo 点为球心、半径 r=1r = 1 的球面 ss 上，分割一小块 Δs\Delta s，以 Δs\Delta s 为底面，以 oo 点为顶点，构成一个圆锥体 hh，则 Δs\Delta s 等于圆锥体h的立体角。

锥体 hh 的立体角 Ω\Omega 大小为锥体的底面积 ΔS\Delta S 与球的半径 rr 平方之比，当 ΔS\Delta S 无限的小，变成了 dSdS，有：

dΩ=dSr2\begin{equation}\nonumber d\Omega = \dfrac{dS}{r^2} \end{equation}

当 r=1r = 1 时候，上式变成了 dΩ=dSd\Omega = dS

以上是用锥体的底面积来定义立体角，现在我们把以上的立体角定义推广，用锥体的体积来定义立体角。

在以 oo 点为球心、半径 r=1r = 1 的球面 ss 上，分割一小块 ΔS\Delta S ，以 ΔS\Delta S 为底面，以 oo 点为顶点，构成一个圆锥体 hh，则圆锥体 hh 的体积 ΔV\Delta V 等于圆锥体 hh 的立体角。

圆锥体 hh 的立体角 Ω\Omega 大小为锥体的体积 ΔV\Delta V 与球的半径 rr 立方之比，当 ΔV\Delta V 无限的小，变成了 dVdV，有：

dΩ=dVr3\begin{equation}\nonumber d\Omega = \dfrac{dV}{r^3} \end{equation}

当 r=1r = 1 时候，上式变成了

dΩ=dV\begin{equation}\nonumber d\Omega = dV \end{equation}
点击展开疑问：上式是否应该写为 dΩ=3 dVd\Omega = 3\ dV ？

有了以上的准备知识，我们来考虑以上的 oo 点在 s′s' 系里，静止时候质量

m′=k ∯dn∯dΩ′\begin{equation}\nonumber m' = k\ \dfrac{\oiint dn}{\oiint d\Omega'} \end{equation}

我们用一个半径为1的单位球体积，在其中分割一个顶点在球心 oo 点上、体积为 dv′dv' 的圆锥体，替代上式中的 dΩ′d\Omega'，则：

m′=k ∯dn∯dv′\begin{equation}\nonumber m' = k\ \dfrac{\oiint dn}{\oiint dv'} \end{equation}

相应的在 ss 系里，oo 点以速度 v⃗\vec{v}【标量为 vv】匀速直线运动的时候，质量

m=k ∯dn∯dv\begin{equation}\nonumber m = k\ \dfrac{\oiint dn}{\oiint dv} \end{equation}

注意，nn 在 s′s' 系和 ss 系里是一样的，也就是 oo 点的运动速度 v⃗\vec{v} 不能改变几何点位移的条数 nn。

我们只要求出 dv′=dx′ dy′ dz′dv'= dx'\ dy'\ dz' 和 dv=dx dy dzdv = dx\ dy\ dz 之间的关系，就可以求出 mm 和 m′m' 之间的关系。

根据相对论中的最简版洛伦兹正变换【因为我们默认了观察者我在 ss 系里，质点 oo 相对于我在运动】：

x′=x−vt1−v2c2y′=yz′=zt′=t−vxc21−v2c2\begin{align} x' &= \dfrac{x - vt}{\sqrt{1 - \dfrac{v^2}{c^2}}}\nonumber \\ y' &= y\nonumber \\ z' &= z\nonumber \\ t' &= \dfrac{t - \dfrac{vx}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}}\nonumber \end{align}

在最简版洛伦兹变换中，由于考察点 oo 点在 s′s' 系中的位置 x′x' 是静止的，在 ss 系里是以速度 v⃗\vec{v} 运动。

我们只有把 ss 系里的时间 tt 取一个固定的时刻，xx 和 x′x' 相互比较才有意义，所以，dt/dx=0dt/dx=0，得出微分式：

点击展开疑问：上面这句解释并没有说清楚为什么 dt/dx=0dt/dx=0
dx′=dx1−v2c2dy′=dydz′=dz\begin{align} dx' &= \dfrac{dx}{\sqrt{1-\dfrac{v^2}{c^2}}} \nonumber \\ dy' &= dy \nonumber \\ dz' &= dz \nonumber \end{align}

由此得出：

m′=k ∯dn∯dv′=k ∯dn∯dx′ dy′ dz′m=k ∯dn∯dv=k ∯dn∯dx dy dz\begin{align} m' &= k\ \dfrac{\oiint dn}{\oiint dv'} = k\ \dfrac{\oiint dn}{\oiint dx'\ dy'\ dz'} \nonumber \\ m &= k\ \dfrac{\oiint dn}{\oiint dv} = k\ \dfrac{\oiint dn}{\oiint dx\ dy\ dz} \nonumber \end{align}

由 ∯dx′ dy′ dz′=11−v2c2∯dx dy dz\oiint dx'\ dy'\ dz' = \dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}\oiint dx\ dy\ dz

可以导出：

m=11−v2c2m′\begin{equation}\nonumber m = \dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}} m' \end{equation}

当 oo 点以速度 v⃗\vec{v} 运动的时候，质量增大了一个相对论因子 11−v2c2\dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}，这个结果和相对论是一致的。

引力场的洛伦兹变换

Section titled 引力场的洛伦兹变换

有了引力场和质量的定义方程，质速关系方程，加上相对论的洛伦兹变换，就可以导出引力场在两个相互匀速直线运动的参考系 s′s' 系和 ss 系之间的变换。

设想惯性参考系 s′s' 相对于 ss 系以速度 v⃗\vec{v}【标量为 vv】沿 xx 轴匀速直线运动运动。在 s′s' 系里，一个静止的很薄的矩形面板，带有质量，在薄板上面产生引力场 A′⃗\vec{A'}

我们让薄板垂直于 xx 轴，

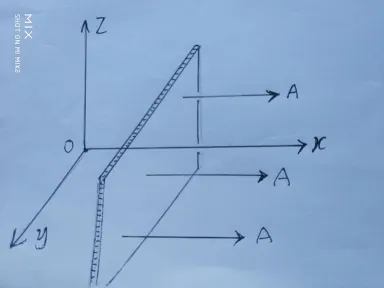
那么在 ss 系里的观察者看来，引力场 A⃗\vec{A} 沿 xx 轴的分量 AxA_x 似乎不会变化。

因为前面的引力场定义方程告诉我们，引力场强度与穿过曲面上空间位移的条数成正比，也就是与密度成正比。这里的薄板的面积没有变化，条数不会变化，密度也就没有变化。

但是，薄板的质量增大了一个相对论因子 1−v2c2\sqrt{1 - \dfrac{v^2}{c^2}}

点击展开修正：上式应取倒数

质量的增大，从几何角度看，应该是空间位移矢量方向与考察的立体角之间的对应变化，所以：

Ax=Ax′1−v2c2\begin{equation}\nonumber A_x = \dfrac{A_x'}{\sqrt{1-\dfrac{v^2}{c^2}}} \end{equation}

Ax′A_x' 为 s′s' 系里引力场 A′⃗\vec{A'} 的沿 x′x' 轴上的分量。

当我们把薄板和 xx 轴平行，

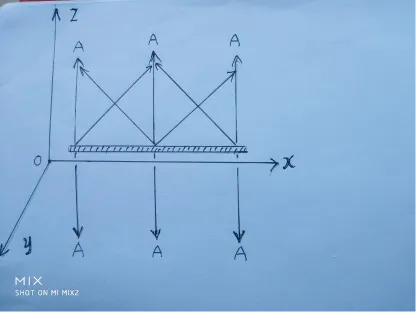
薄板要收缩一个相对论因子，加上质量增大一个相对论因子。注意，图中倾斜的引力场线在 xx 轴上的投影的分量正反相互抵消为零。所以，我们得到了：

Ax=0Ay=Ay′1−v2c2Az=Az′1−v2c2\begin{align} A_x &= 0 \nonumber \\ A_y &= \dfrac{A_y'}{1-\dfrac{v^2}{c^2}} \nonumber \\ A_z &= \dfrac{A_z'}{1-\dfrac{v^2}{c^2}} \nonumber \end{align}

Ay′A_y' 和 Az′A_z' 是 s′s' 系里引力场 A′⃗\vec{A'} 在 y′y' 轴和 z′z' 轴上两个分量。

由前面的引力场定义方程，我们得到：

Ax′=−G m′ x′(r′)3Ay′=−G m′ y′(r′)3Az′=−G m′ z′(r′)3\begin{align} A_x' &= - \dfrac{G\ m'\ x'}{(r')^3} \nonumber \\ A_y' &= - \dfrac{G\ m'\ y'}{(r')^3} \nonumber \\ A_z' &= - \dfrac{G\ m'\ z'}{(r')^3} \nonumber \end{align}

由此导出：

Ax=−G m′ x′1−v2c2 r′3Ay=−G m′ y′(1−v2c2) r′3Az=−G m′ z′(1−v2c2) r′3\begin{align} A_x &= - \dfrac{G\ m'\ x'}{\sqrt{1-\dfrac{v^2}{c^2}}\ {r'}^3} \nonumber \\ A_y &= - \dfrac{G\ m'\ y'}{(1-\dfrac{v^2}{c^2})\ {r'}^3} \nonumber \\ A_z &= - \dfrac{G\ m'\ z'}{(1-\dfrac{v^2}{c^2})\ {r'}^3} \nonumber \end{align}

由此得到：

Ax=−G m γ x−vt[γ2(x−vt)2+y2+z2]32Ay=−G m γ y[γ2(x−vt)2+y2+z2]32Az=−G m γ z[γ2(x−vt)2+y2+z2]32\begin{align} A_x &= - G\ m\ \gamma\ \dfrac{x - vt}{[\gamma^2(x-vt)^2+y^2+z^2]^{\frac{3}{2}}} \nonumber \\ A_y &= - G\ m\ \gamma\ \dfrac{y}{[\gamma^2(x-vt)^2+y^2+z^2]^{\frac{3}{2}}} \nonumber \\ A_z &= - G\ m\ \gamma\ \dfrac{z}{[\gamma^2(x-vt)^2+y^2+z^2]^{\frac{3}{2}}} \nonumber \end{align}

由此得到：

A⃗=−G m γ (x−vt)i⃗+yj⃗+zk⃗[γ2(x−vt)2+y2+z2]32\begin{equation}\nonumber \vec{A} = - G\ m\ \gamma\ \dfrac{(x - vt)\vec{i} + y\vec{j} + z\vec{k}}{[\gamma^2(x-vt)^2+y^2+z^2]^{\frac{3}{2}}} \end{equation}

令 θ\theta 为矢径 r⃗\vec{r}【标量为 r=γ2(x−vt)2+y2+z2r = \sqrt{\gamma^2(x-vt)^2+y^2+z^2} 】和速度 v⃗\vec{v}【标量为 vv】之间的夹角，A⃗\vec{A} 可以表示为极坐标形式：

A⃗=−G mγ2 r2(1−β2 sin2θ)32 er⃗\begin{equation}\nonumber \vec{A} = - \dfrac{G\ m}{\gamma^2\ r^2(1 - \beta^2\ sin^2\theta)^{\frac{3}{2}}}\ \vec{e_r} \end{equation}

式中 GG 为万有引力常数, γ=11−v2c2\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} ，β=vc\beta = \dfrac{v}{c}，er⃗\vec{e_r} 是矢径 r⃗\vec{r}（标量为 rr )的单位矢量。

这个结果和电场的相对论变换形式是一样，这个表明，高斯定理适用于静止引力场，也适用于匀速直线运动的引力场。

在 s′s' 系里有，

∇⃗⋅A′⃗=∂Ax′∂x′+∂Ay′∂y′+∂Az′∂z′=G m′dV′\begin{equation}\nonumber \vec{\nabla} \cdot \vec{A'} = \dfrac{\partial{A_x'}}{\partial{x'}} + \dfrac{\partial{A_y'}}{\partial{y'}} + \dfrac{\partial{A_z'}}{\partial{z'}} = \dfrac{G\ m'}{dV'} \end{equation}

在 ss 系里有：

∇⃗⋅A⃗=∂Ax∂x+∂Ay∂y+∂Az∂z=G mdV\begin{equation}\nonumber \vec{\nabla} \cdot \vec{A} = \dfrac{\partial{A_x}}{\partial{x}} + \dfrac{\partial{A_y}}{\partial{y}} + \dfrac{\partial{A_z}}{\partial{z}} = \dfrac{G\ m}{dV} \end{equation}

其中 GG 是万有引力常数，s′s' 系里的 dV′=dx′ dy′ dz′dV' = dx'\ dy'\ dz' ，质量为 m′m'， ss 系里的 dV=dx dy dzdV = dx\ dy\ dz，质量为 mm。

由以上的引力场变换，可以证明这两个高斯公式都能够成立，高斯定理不仅适用于静止物体的静止引力场，同样适用于运动物体的引力场。

注意，式中 γdx=dx′\gamma dx = dx' 是从洛伦兹正变换 x′=γ(x−vt)x' = \gamma(x - v t) 求微分得到的。

点击展开疑问：为什么可以将 dtdt 那一项丢掉
Edit this page Translate this page
Contribute Community