点击展开注解:本节导读
这一部分其实在推导 v ⃗ \vec{v} v c ⃗ \vec{c} c
另外,下面的变量命名也存在各种细节问题,比如:既把 x x x p p p s s s
设有两个直角惯性坐标系 s s s s ′ s' s ′ p p p s s s s ′ s' s ′ ( x , y , z , t ) (x, y, z, t) ( x , y , z , t ) ( x ′ , y ′ , z ′ , t ′ ) (x', y', z', t') ( x ′ , y ′ , z ′ , t ′ )
本文重点讨论洛伦兹变换的最简情况,就是考察点 p p p s ′ s' s ′
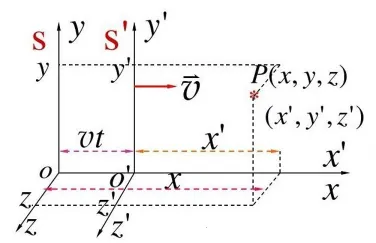
在下图中,
x x x x ′ x' x ′ t ′ = t = 0 t' = t = 0 t ′ = t = 0 s s s o o o s s s o o o s ′ s' s ′ o ′ o' o ′ s ′ s' s ′ o ′ o' o ′
随后,o ′ o' o ′ o o o v v v x x x
设想在某时刻,发生了一次爆炸事件,在 s ′ s' s ′ p p p x ′ , y ′ , z ′ , t ′ x', y', z', t' x ′ , y ′ , z ′ , t ′
也就是爆炸事件发生在 t ′ t' t ′ p p p x ′ x' x ′ o ′ o' o ′ x ′ x' x ′ p p p s ′ s' s ′
在 s s s p p p x , y , z x, y, z x , y , z t t t
也就是爆炸发生在 t t t x x x o o o x x x p p p s s s v v v
我们来求出发生在 p p p
在上图中,可以直观的看出:
x ′ = x − v t x = x ′ + v t ′ \begin{align}
x' &= x - vt \nonumber \\
x &= x' + vt' \nonumber
\end{align} x ′ x = x − v t = x ′ + v t ′ 按照伽利略相对性原理的思想,时间、空间长度的测量与观测者的运动速度 v v v t = t ′ t = t' t = t ′
但是,相对论认为时间、空间长度的测量与观测者的相互运动速度 v v v v v v
在 s s s x ′ = x − v t x' = x - vt x ′ = x − v t x ′ x' x ′ 1 k \dfrac{1}{k} k 1
1 k x ′ = x − v t \begin{equation}\nonumber
\dfrac{1}{k}x' = x - vt
\end{equation} k 1 x ′ = x − v t 所以有:
x ′ = k ( x − v t ) \begin{equation}\tag{21.1}
x' = k(x - vt)
\end{equation} x ′ = k ( x − v t ) ( 21.1 ) 在 s ′ s' s ′ x = x ′ + v t ′ x = x' + vt' x = x ′ + v t ′ x x x 1 k \dfrac{1}{k} k 1
1 k x = x ′ + v t ′ \begin{equation}\nonumber
\dfrac{1}{k}x = x' + vt'
\end{equation} k 1 x = x ′ + v t ′ 所以有:
x = k ( x ′ + v t ′ ) \begin{equation}\tag{21.2}
x = k(x' + vt')
\end{equation} x = k ( x ′ + v t ′ ) ( 21.2 ) 由于 s s s s ′ s' s ′ x ′ x' x ′ ( x − v t ) (x-vt) ( x − v t ) x x x ( x ′ + v t ′ ) (x'+vt') ( x ′ + v t ′ )
点击展开疑问:关于上述论述的严谨性 相对论的相对性原理认为:物理定律在所有的惯性参考系中都是相同或者平权的,不同惯性系的物理方程形式应该是相同的。
所以 ( 21.1 ) (21.1) ( 21.1 ) ( 21.2 ) (21.2) ( 21.2 ) k k k
对于 k k k
设想由原点 o o o o ′ o' o ′ c c c
设该光束的波前【或者叫光子、空间点】p p p s s s ( x , y , z , t ) (x, y, z, t) ( x , y , z , t ) s ′ s' s ′ ( x ′ , y ′ , z ′ , t ′ ) (x', y', z', t') ( x ′ , y ′ , z ′ , t ′ )
以该光束的波前【或者叫光子、空间点】p p p
如果光速 c c c s s s s ′ s' s ′
x = c t x ′ = c t ′ \begin{align}
x &= ct \tag{21.3} \\
x' &= ct' \tag{21.4}
\end{align} x x ′ = c t = c t ′ ( 21.3 ) ( 21.4 ) 将 ( 21.1 ) , ( 21.2 ) , ( 21.3 ) , ( 21.4 ) (21.1), (21.2), (21.3), (21.4) ( 21.1 ) , ( 21.2 ) , ( 21.3 ) , ( 21.4 )
c t ′ = k ( x − v t ) c t = k ( x ′ + v t ′ ) \begin{align}
ct' &= k(x - vt) \nonumber \\
ct &= k(x' + vt') \nonumber
\end{align} c t ′ c t = k ( x − v t ) = k ( x ′ + v t ′ ) 将上边两式相乘可以导出:
c 2 t t ′ = k 2 ( x − v t ) ( x ′ + v t ′ ) = k 2 ( x x ′ + x v t ′ − v t x ′ − v 2 t t ′ ) = k 2 ( x x ′ + c t v t ′ − v t c t ′ − v 2 t t ′ ) = k 2 ( c 2 t t ′ − v 2 t t ′ ) \begin{equation}\nonumber
\begin{aligned}
c^2tt' &= k^2(x - vt)(x' + vt') \\
&= k^2(xx' + xvt' - vtx' - v^2tt') \\
&= k^2(xx' + ctvt' - vtct' - v^2tt') \\
&= k^2(c^2tt' - v^2tt')
\end{aligned}
\end{equation} c 2 t t ′ = k 2 ( x − v t ) ( x ′ + v t ′ ) = k 2 ( x x ′ + xv t ′ − v t x ′ − v 2 t t ′ ) = k 2 ( x x ′ + c t v t ′ − v t c t ′ − v 2 t t ′ ) = k 2 ( c 2 t t ′ − v 2 t t ′ ) 再一次导出:
c 2 = k 2 ( c 2 − v 2 ) k = 1 1 − v 2 c 2 \begin{align}
c^2 &= k^2(c^2 - v^2) \nonumber \\
k &= \dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}} \nonumber
\end{align} c 2 k = k 2 ( c 2 − v 2 ) = 1 − c 2 v 2 1 将上式带入 ( 21.1 ) (21.1) ( 21.1 ) ( 21.2 ) (21.2) ( 21.2 )
x ′ = x − v t 1 − v 2 c 2 x = x ′ + v t ′ 1 − v 2 c 2 \begin{align}
x' &= \dfrac{x - vt}{\sqrt{1 - \dfrac{v^2}{c^2}}} \tag{21.5} \\
x &= \dfrac{x' + vt'}{\sqrt{1 - \dfrac{v^2}{c^2}}} \tag{21.6} \\
\end{align} x ′ x = 1 − c 2 v 2 x − v t = 1 − c 2 v 2 x ′ + v t ′ ( 21.5 ) ( 21.6 ) 由 ( 21.5 ) (21.5) ( 21.5 ) ( 21.6 ) (21.6) ( 21.6 ) x ′ x' x ′
t ′ = t − v x c 2 1 − v 2 c 2 \begin{equation}
t' = \dfrac{t-\dfrac{vx}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}} \tag{21.7}
\end{equation} t ′ = 1 − c 2 v 2 t − c 2 vx ( 21.7 ) 由 ( 21.5 ) (21.5) ( 21.5 ) ( 21.6 ) (21.6) ( 21.6 ) x x x
t = t ′ + v x ′ c 2 1 − v 2 c 2 \begin{equation}
t = \dfrac{t'+\dfrac{vx'}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}} \tag{21.8}
\end{equation} t = 1 − c 2 v 2 t ′ + c 2 v x ′ ( 21.8 ) 式:
x ′ = x − v t 1 − v 2 c 2 y ′ = y z ′ = z t ′ = t − v x c 2 1 − v 2 c 2 \begin{align}
x' &= \dfrac{x - vt}{\sqrt{1 - \dfrac{v^2}{c^2}}}\nonumber \\
y' &= y\nonumber \\
z' &= z\nonumber \\
t' &= \dfrac{t - \dfrac{vx}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}}\nonumber
\end{align} x ′ y ′ z ′ t ′ = 1 − c 2 v 2 x − v t = y = z = 1 − c 2 v 2 t − c 2 vx 这就是洛伦兹正变换。
式:
x = x ′ + v t ′ 1 − v 2 c 2 y = y ′ z = z ′ t = t ′ + v x ′ c 2 1 − v 2 c 2 \begin{align}
x &= \dfrac{x' + vt'}{\sqrt{1 - \dfrac{v^2}{c^2}}}\nonumber \\
y &= y'\nonumber \\
z &= z'\nonumber \\
t &= \dfrac{t' + \dfrac{vx'}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}}\nonumber
\end{align} x y z t = 1 − c 2 v 2 x ′ + v t ′ = y ′ = z ′ = 1 − c 2 v 2 t ′ + c 2 v x ′ 就是洛伦兹逆变换。
注意,洛伦兹变换中 y y y z z z
下面我们用时间物理定义,来解释 ( 21.3 ) (21.3) ( 21.3 ) ( 21.4 ) (21.4) ( 21.4 )
按照前面的时间物理定义。
s ′ s' s ′ p p p o ′ o' o ′ o o o o o o o ′ o' o ′ c c c x ′ x' x ′ x x x x x x x ′ x' x ′ t ′ t' t ′ x ′ x' x ′ p p p x ′ t ′ = c \dfrac{x'}{t'} = c t ′ x ′ = c
s s s p p p o o o o ′ o' o ′ o o o o ′ o' o ′ x x x x ′ x' x ′ x x x x ′ x' x ′ t t t x x x p p p
以上的时间物理定义告诉我们:时间与观测者周围空间中一个空间点 p p p
所以,s s s t t t s ′ s' s ′ t ′ t' t ′ s s s x x x s ′ s' s ′ x ′ x' x ′
t t ′ = x x ′ \begin{equation}\nonumber
\dfrac{t}{t'} = \dfrac{x}{x'}
\end{equation} t ′ t = x ′ x 将上式作一个变换,
x t = x ′ t ′ \begin{equation}\nonumber
\dfrac{x}{t} = \dfrac{x'}{t'}
\end{equation} t x = t ′ x ′ 由于 x t \dfrac{x}{t} t x x ′ t ′ \dfrac{x'}{t'} t ′ x ′ x ′ t ′ = c \dfrac{x'}{t'} = c t ′ x ′ = c
x t = x ′ t ′ = 速率 = c \begin{equation}\nonumber
\dfrac{x}{t} = \dfrac{x'}{t'} = \text{速率} = c
\end{equation} t x = t ′ x ′ = 速率 = c 点击展开注解:关于上述“量纲是速率”的表述 所以,以上说明了一定会有一个与时间密切相关的特殊速率【我们用 c c c c c c
以上的时间物理定义只要是正确的,就一定能够证明 ( 21.3 ) (21.3) ( 21.3 ) ( 21.4 ) (21.4) ( 21.4 ) c c c
接下来我们用统一场论思想对以上洛伦兹变换做出解读。
洛伦兹变换继承了伽利略变换中 s s s s ′ s' s ′ v v v s ′ s' s ′ s s s − v - v − v
统一场论认为一切运动形式、物理现象都是我们观察者描述出来的,剔除了我们观察者,谈论物理现象、运动状态是没有意义的。
s ′ s' s ′ s s s
s ′ s' s ′ s s s s ′ s' s ′ s s s
统一场论认为,描述运动需要存在4个基本条件:一个是空间;一个是时间,包括时间的开始时刻、过程、结束时刻;一个是观察者;一个是被描述的对象,也就是物体或者由物体运动变化所形成的事件。
s ′ s' s ′ s s s p p p s ′ s' s ′ s s s s s s s ′ s' s ′
当我这个观察者被默认站在 s s s p p p s ′ s' s ′ p p p
我们还有一个问题:就一个参考系来讲,为什么光速也是常数?
这一点可以这样理解,时间完全的等价于观测者周围空间的运动,也就是:
运动的空间 = 时间。
为了在物理上使“运动的空间 = 时间”成立时量纲不发生混乱,我们需要在时间前面乘上不随时间、运动空间变化的一个常数——光速,
运动的空间 = 光速乘以时间。
从数学的角度看,一个变量对自身求导数,结果是1或者其它常数。
点击展开注解:本节导读 可能有人认为光线可以向任意方向跑啊,那空间岂不是也向任意方向跑吗?描述任何运动需有参照物,空间的运动又是参照谁呢?
在统一场论中,物体周围的空间的确是以物体为中心,向四周发散运动。
空间的运动是参照物体的,我们描述空间的运动都是指某个物体周围空间是如何运动的。
特殊情况下,没有物体,我们描述空间的运动是相对我们人的身体。
没有任何物体的情况下,单纯的描述空间的运动是没有意义的。
下面我们再来考虑在空间点运动方向与观察对象的运动速度 v v v
在下图中,x x x x ′ x' x ′ t ′ = t = 0 t'= t = 0 t ′ = t = 0 s s s o o o s s s o o o s ′ s' s ′ o ′ o' o ′ s ′ s' s ′ o ′ o' o ′
随后,o ′ o' o ′ o o o v ⃗ \vec{v} v v v v x x x
设想有一个质点 o ′ o' o ′ s ′ s' s ′ o ′ o' o ′
在零时刻,s ′ s' s ′ p p p o ′ o' o ′ t ′ t' t ′ c c c y ′ y' y ′ o ′ p o'p o ′ p o ′ p t ′ = c \dfrac{o'p}{t'} = c t ′ o ′ p = c p p p p p p
空间点 p p p p p p s s s p p p t t t o p op o p
点击展开注解:关于一个字母表示多种含义的问题 o p op o p o ′ p o'p o ′ p 有用的时间 t t t t ′ t' t ′
因为,按照时间的物理定义,时间与空间点 p p p
O P O ′ P = t t ′ \begin{equation}\nonumber
\dfrac{OP}{O'P} = \dfrac{t}{t'}
\end{equation} O ′ P OP = t ′ t 将上式变形得到:
O P t = O ′ P t ′ \begin{equation}\nonumber
\dfrac{OP}{t} = \dfrac{O'P}{t'}
\end{equation} t OP = t ′ O ′ P 由 O ′ P t ′ = c \dfrac{O'P}{t'} = c t ′ O ′ P = c
O P t = O ′ P t ′ = c \begin{equation}\nonumber
\dfrac{OP}{t} = \dfrac{O'P}{t'} = c
\end{equation} t OP = t ′ O ′ P = c 上式就解释了光速为什么会相对于两个相互运动观测者的数值是不变的。
我们再来求出 t t t t ′ t' t ′
O P t = O ′ P t ′ = c O P = O ′ P 2 + v 2 t 2 \begin{align}
\dfrac{OP}{t} = \dfrac{O'P}{t'} = c \nonumber \\
OP = \sqrt{O'P^2 + v^2t^2} \nonumber
\end{align} t OP = t ′ O ′ P = c OP = O ′ P 2 + v 2 t 2 可以得到:
t ′ = t 1 − v 2 c 2 \begin{equation}\nonumber
t' = t\sqrt{1-\dfrac{v^2}{c^2}}
\end{equation} t ′ = t 1 − c 2 v 2 可以得到微分形式:
d t d t ′ = 1 1 − v 2 c 2 \begin{equation}\nonumber
\dfrac{dt}{dt'} = \dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}
\end{equation} d t ′ d t = 1 − c 2 v 2 1 相对论认为,发生了某一个事情,观察者相对于这个事情发生的地点是静止的,也就是事件开始时刻和结束时刻都在同一个地点,测量这个事情所经历的时间是固有时间,也就是以上的 t ′ t' t ′
相对论中固有时间最短,这个结果和相对论的结果是一样的。
我们将洛伦兹逆变换
t = t ′ + v x ′ c 2 1 − v 2 c 2 \begin{equation}\nonumber
t = \dfrac{t' + \dfrac{vx'}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}}
\end{equation} t = 1 − c 2 v 2 t ′ + c 2 v x ′ 两边对时间 t ′ t' t ′
d t d t ′ = 1 1 − v 2 c 2 \begin{equation}\nonumber
\dfrac{dt}{dt'} = \dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}
\end{equation} d t ′ d t = 1 − c 2 v 2 1 注意,式中的 x ′ x' x ′ t ′ t' t ′ x ′ x' x ′ t ′ t' t ′ s ′ s' s ′ s ′ s' s ′ p p p x ′ x' x ′
我们将洛伦兹正变换
t ′ = t − v x c 2 1 − v 2 c 2 \begin{equation}\nonumber
t' = \dfrac{t - \dfrac{vx}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}}
\end{equation} t ′ = 1 − c 2 v 2 t − c 2 vx 两边对时间 t t t
d t ′ d t = 1 − v 2 c 2 1 − v 2 c 2 = 1 − v 2 c 2 \begin{equation}\nonumber
\dfrac{dt'}{dt} = \dfrac{1-\dfrac{v^2}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}} = \sqrt{1-\dfrac{v^2}{c^2}}
\end{equation} d t d t ′ = 1 − c 2 v 2 1 − c 2 v 2 = 1 − c 2 v 2 所以,有:
d t d t ′ = 1 1 − v 2 c 2 \begin{equation}\nonumber
\dfrac{dt}{dt'} = \dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}
\end{equation} d t ′ d t = 1 − c 2 v 2 1 注意,式中的 x x x p p p s s s t t t
d x d t = v \begin{equation}\nonumber
\dfrac{dx}{dt} = v
\end{equation} d t d x = v 因此
d ( v x c 2 ) d t = v 2 c 2 \begin{equation}\nonumber
\dfrac{d(\dfrac{vx}{c^2})}{dt} = \dfrac{v^2}{c^2}
\end{equation} d t d ( c 2 vx ) = c 2 v 2 因为 x x x t t t s s s s s s p p p x x x v v v
这个结果和以上是一样的。
我们还有一个疑问:
空间点 p p p y y y s s s s ′ s' s ′
这一切狭义相对论用火车钻山洞的假想试验给出了证明:
设想有一个山洞,外面停一辆火车,车厢高度与洞顶高度相等,现在使火车匀速的开进山洞,运动的火车的高度是否发生变化?
假设火车的高度由于运动变小了,这样,站在地面的观测者认为火车由于运动,高度变小,山洞由于不运动,高度不变,火车肯定顺利的开进山洞。
但是,在火车里面的观测者认为,火车是静止的,因而火车高度不变,山洞是运动的,山洞的高度会降低,火车无法通过山洞,这就发生了矛盾。
但是,火车能否开进山洞是一个确定的物理事实,不应该与观测者的选择有关,唯一合理的观点是:
匀速直线运动不能够使运动垂直方向上的空间长度缩短,同样的道理,也不能伸长,结果是不变。
可能人们还有一个疑问:观测者周围空间有许多空间点,为什么一个空间点的运动就可以表示时间?
这个应该这样理解,时间反映了空间运动的一种性质,我们观测者通过描述空间中许多空间点的其中一个,就可以把空间具有时间这种变化的性质给表现来,这个也表明了,时间不能够脱离观测者而独立存在。
我们前面引入了矢量光速概念,但没有深入的讨论。
光速能不能看成矢量,相对论中没有深入讨论,按照相对论,光速与光源的运动速度无关,与观测者的选择无关,与时间无关,与空间位置无关,纯粹一个常数。
所以,相对论倾向认为光速不能够看成矢量,换句话,在相对论中讨论光速的矢量性是没有意义的。
光速是常数最早来自于麦克斯韦电磁波波动方程,波动方程中的光速以常数出现。
统一场论提出了与之不同的观点,认为光速在某些情况下可以表现为矢量,其方向和光源的运动速度有着函数关系。
统一场论为了区分,把矢量光速叫光速度,用 c ⃗ \vec{c} c c ⃗ \vec{c} c ∣ c ⃗ ∣ |\vec{c}| ∣ c ∣
光速速率叫光速率,又叫标量光速,用 c c c c c c
矢量光速 c ⃗ \vec{c} c x , y , z x, y, z x , y , z c x ⃗ , c y ⃗ , c z ⃗ \vec{c_x}, \vec{c_y}, \vec{c_z} c x , c y , c z
在统一场论中,光源的运动速度 v ⃗ \vec{v} v c ⃗ \vec{c} c
我们先考虑一种特殊的情况。
我们令矢量光速 c ⃗ \vec{c} c v ⃗ \vec{v} v θ = π 2 − β \theta = \dfrac{\pi}{2} - \beta θ = 2 π − β
我们先来大致判断一下 v ⃗ \vec{v} v v v v β \beta β
从相对论中我们知道,由光速不变可以推导出:v ⃗ \vec{v} v v ⃗ \vec{v} v v ⃗ \vec{v} v
统一场论中,c ⃗ \vec{c} c
随着 v ⃗ \vec{v} v c ⃗ \vec{c} c β \beta β v v v β = 90 ° \beta = 90° β = 90° v ⃗ \vec{v} v v v v c c c
所以,β \beta β v ⃗ \vec{v} v v v v 0 0 0 c c c
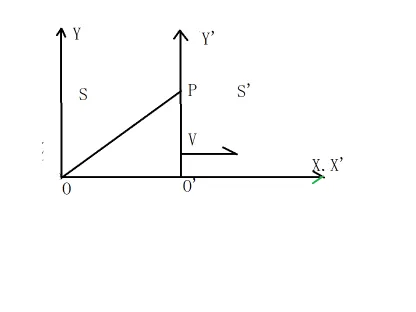
在下图中:
二维直角坐标系 s s s o o o s ′ s' s ′ o ′ o' o ′ 0 0 0 x x x x ′ x' x ′
后来,相互以匀速度 v ⃗ \vec{v} v v v v x x x
一个质点 o o o s ′ s' s ′ o ′ o' o ′ s s s s ′ s' s ′ p p p
p p p o o o y ′ y' y ′
如果我们把光看成是光子,这里的质点 o o o p p p p p p
在统一场论中,把光看成是激发电子随空间一同运动,即使没有激发电子,或者没有光子,质点 o o o c ⃗ \vec{c} c
后一种情况下,p p p p p p o o o
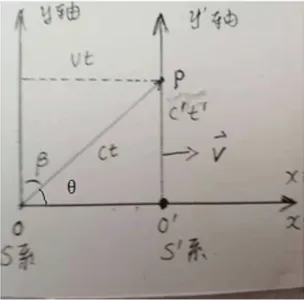
s ′ s' s ′ p p p o o o t ′ t' t ′ p p p c ′ ⃗ \vec{c'} c ′ o ′ p → = c ′ ⃗ t ′ \overrightarrow{o'p} = \vec{c'}t' o ′ p = c ′ t ′
s s s p p p t t t c ⃗ \vec{c} c c c c o p = c t op = ct o p = c t
在上图中可以看出:
∣ v ⃗ t ∣ ∣ c ⃗ t ∣ = s i n β = v c \begin{equation}\nonumber
\dfrac{|\vec{v}t|}{|\vec{c}t|} = sin\beta = \dfrac{v}{c}
\end{equation} ∣ c t ∣ ∣ v t ∣ = s in β = c v 消除 t t t
∣ v ⃗ ∣ ∣ c ⃗ ∣ = s i n β = v c \begin{equation}\nonumber
\dfrac{|\vec{v}|}{|\vec{c}|} = sin\beta = \dfrac{v}{c}
\end{equation} ∣ c ∣ ∣ v ∣ = s in β = c v 由于 c ⃗ \vec{c} c v ⃗ \vec{v} v θ = π 2 − β \theta = \dfrac{\pi}{2} - \beta θ = 2 π − β
c o s θ = ∣ v ⃗ ∣ ∣ c ⃗ ∣ = v c \begin{equation}\nonumber
cos\theta = \dfrac{|\vec{v}|}{|\vec{c}|} = \dfrac{v}{c}
\end{equation} cos θ = ∣ c ∣ ∣ v ∣ = c v 由上式可以导出
s i n θ = 1 − v 2 c 2 \begin{equation}\nonumber
sin\theta = \sqrt{1 - \dfrac{v^2}{c^2}}
\end{equation} s in θ = 1 − c 2 v 2 这个实际上就是相对论因子产生的原因。
对以上分析,可以得出如下看法:
在 v ⃗ \vec{v} v v v v v ⃗ \vec{v} v c ⃗ \vec{c} c v ⃗ \vec{v} v v v v c ⃗ \vec{c} c v v v c ⃗ \vec{c} c c c c c ⃗ \vec{c} c
光源运动速度 v ⃗ \vec{v} v v ⃗ \vec{v} v c ⃗ \vec{c} c
垂直原理告诉我们,空间的垂直状态【90度角】可以导致运动。
其逆定理是:运动又可以导致空间的垂直状态发生倾斜,运动速度达到光速的时候,垂直状态彻底消失【躺平】。
以上公式 s i n β = v c sin\beta = \dfrac{v}{c} s in β = c v c o s θ = v c cos\theta = \dfrac{v}{c} cos θ = c v
垂直原理的实质是空间的角度和运动速度有等价性和互补性。
以上只是分析了特殊情况下,矢量光速 c ⃗ \vec{c} c v ⃗ \vec{v} v v v v
揭示它们之间普遍关系,需要矢量光速 c ⃗ \vec{c} c s ′ s' s ′ s s s
在 s ′ s' s ′ c ′ ⃗ \vec{c'} c ′ c x ′ ⃗ , c y ′ ⃗ , c z ′ ⃗ \vec{c'_x}, \vec{c'_y}, \vec{c'_z} c x ′ , c y ′ , c z ′
在 s s s c ⃗ \vec{c} c c x ⃗ , c y ⃗ , c z ⃗ \vec{c_x}, \vec{c_y}, \vec{c_z} c x , c y , c z
利用相对论的速度正变换【我们以上已经证明洛伦兹变换是正确的,而相对论速度变换是对洛伦兹变换求时间导数得到的,因而相对论速度变换是可以用的】可以导出 c ′ ⃗ \vec{c'} c ′ c ⃗ \vec{c} c
c x ′ = c x − v 1 − c x v c 2 c y ′ = c y 1 − v 2 c 2 1 − c x v c 2 c z ′ = c z 1 − v 2 c 2 1 − c x v c 2 \begin{align}
c'_x &= \dfrac{c_x-v}{1-\dfrac{c_x v}{c^2}} \nonumber \\
c'_y &= \dfrac{c_y\sqrt{1-\dfrac{v^2}{c^2}}}{1-\dfrac{c_x v}{c^2}} \nonumber \\
c'_z &= \dfrac{c_z\sqrt{1-\dfrac{v^2}{c^2}}}{1-\dfrac{c_x v}{c^2}} \nonumber
\end{align} c x ′ c y ′ c z ′ = 1 − c 2 c x v c x − v = 1 − c 2 c x v c y 1 − c 2 v 2 = 1 − c 2 c x v c z 1 − c 2 v 2 点击展开注解:关于上述公式的推导 由以上可以导出:
c x ′ 2 + c y ′ 2 + c z ′ 2 = ( c x − v ) 2 + c y 2 ( 1 − v 2 c 2 ) + c z 2 ( 1 − v 2 c 2 ) ( 1 − c x v c 2 ) 2 = c 4 [ c x 2 + c y 2 + c z 2 − 2 c x v + v 2 − ( c y 2 + c z 2 ) v 2 c 2 ] ( c 2 − c x v ) 2 = c 4 [ c 2 − 2 c x v + v 2 − ( c 2 − c x 2 ) v 2 c 2 ] ( c 2 − c x v ) 2 = c 4 [ c 2 − 2 c x v + c x 2 v 2 c 2 ] ( c 2 − c x v ) 2 = c 2 ( c 4 − 2 c 2 c x v + c x 2 v 2 ) ( c 2 − c x v ) 2 = c 2 \begin{equation}\nonumber
\begin{aligned}
{c'_x}^2 + {c'_y}^2 + {c'_z}^2 &= \dfrac{(c_x - v)^2 + c_y^2(1-\dfrac{v^2}{c^2}) + c_z^2(1-\dfrac{v^2}{c^2})}{(1-\dfrac{c_xv}{c^2})^2} \\
&= \dfrac{c^4[c_x^2+c_y^2+c_z^2-2c_xv+v^2-(c_y^2+c_z^2)\dfrac{v^2}{c^2}]}{(c^2-c_xv)^2} \\
&= \dfrac{c^4[c^2-2c_xv+v^2-(c^2-c_x^2)\dfrac{v^2}{c^2}]}{(c^2-c_xv)^2} \\
&= \dfrac{c^4[c^2-2c_xv+\dfrac{c_x^2v^2}{c^2}]}{(c^2-c_xv)^2} \\
&= \dfrac{c^2(c^4-2c^2c_xv+c_x^2v^2)}{(c^2-c_xv)^2} \\
&= c^2
\end{aligned}
\end{equation} c x ′ 2 + c y ′ 2 + c z ′ 2 = ( 1 − c 2 c x v ) 2 ( c x − v ) 2 + c y 2 ( 1 − c 2 v 2 ) + c z 2 ( 1 − c 2 v 2 ) = ( c 2 − c x v ) 2 c 4 [ c x 2 + c y 2 + c z 2 − 2 c x v + v 2 − ( c y 2 + c z 2 ) c 2 v 2 ] = ( c 2 − c x v ) 2 c 4 [ c 2 − 2 c x v + v 2 − ( c 2 − c x 2 ) c 2 v 2 ] = ( c 2 − c x v ) 2 c 4 [ c 2 − 2 c x v + c 2 c x 2 v 2 ] = ( c 2 − c x v ) 2 c 2 ( c 4 − 2 c 2 c x v + c x 2 v 2 ) = c 2 由此导出矢量光速 c ⃗ \vec{c} c c ′ ⃗ \vec{c'} c ′
c ′ ⃗ ⋅ c ′ ⃗ = c ⃗ ⋅ c ⃗ = c 2 \begin{equation}\nonumber
\vec{c'} \cdot \vec{c'} = \vec{c} \cdot \vec{c} = c^2
\end{equation} c ′ ⋅ c ′ = c ⋅ c = c 2 c ⃗ \vec{c} c c ′ ⃗ \vec{c'} c ′
以上没有完全讲明白 c ⃗ \vec{c} c v ⃗ \vec{v} v
现在设想有两个观察者分别在 s s s ( x , y , z , t ) (x, y, z, t) ( x , y , z , t ) s ′ s' s ′ ( x ′ , y ′ , z ′ , t ′ ) (x', y', z', t') ( x ′ , y ′ , z ′ , t ′ ) s s s s ′ s' s ′ v ⃗ \vec{v} v x x x
设想在时刻 t = t ′ = 0 t = t'= 0 t = t ′ = 0 s s s s ′ s' s ′ o o o o ′ o' o ′ p p p 0 0 0 o o o o ′ o' o ′ p p p
将式
r ⃗ ( t ) = c ⃗ t = x i ⃗ + y j ⃗ + z k ⃗ \begin{equation}\nonumber
\vec{r}(t) = \vec{c}t = x\vec{i} + y\vec{j} + z\vec{k}
\end{equation} r ( t ) = c t = x i + y j + z k 对自身点乘,结果为:
r 2 = c 2 t 2 = x 2 + y 2 + z 2 \begin{equation}\nonumber
r^2 = c^2t^2 = x^2 + y^2 + z^2
\end{equation} r 2 = c 2 t 2 = x 2 + y 2 + z 2 r r r r ⃗ \vec{r} r r r r s s s p p p
以上方程在相对论中也出现过,相对论中被认为是四维时空距离。
同样的道理,可以导出在 s ′ s' s ′ p p p o ′ o' o ′
r ′ 2 = c 2 t ′ 2 = x ′ 2 + y ′ 2 + z ′ 2 \begin{equation}\nonumber
r'^2 = c^2t'^2 = x'^2 + y'^2 + z'^2
\end{equation} r ′2 = c 2 t ′2 = x ′2 + y ′2 + z ′2 由 r 2 = c 2 t 2 = x 2 + y 2 + z 2 r^2 = c^2t^2 = x^2 + y^2 + z^2 r 2 = c 2 t 2 = x 2 + y 2 + z 2
c 2 t 2 − ( x 2 + y 2 + z 2 ) = 0 \begin{equation}\nonumber
c^2t^2 - (x^2 + y^2 + z^2) = 0
\end{equation} c 2 t 2 − ( x 2 + y 2 + z 2 ) = 0 由 r ′ 2 = c 2 t ′ 2 = x ′ 2 + y ′ 2 + z ′ 2 r'^2 = c^2t'^2 = x'^2 + y'^2 + z'^2 r ′2 = c 2 t ′2 = x ′2 + y ′2 + z ′2
c 2 t ′ 2 − ( x ′ 2 + y ′ 2 + z ′ 2 ) = 0 \begin{equation}\nonumber
c^2t'^2 - (x'^2 + y'^2 + z'^2) = 0
\end{equation} c 2 t ′2 − ( x ′2 + y ′2 + z ′2 ) = 0 由以上方程可以得出时空间隔在相对匀速直线运动的两个惯性系里是不变的。
统一场论认为时空间隔的不变性,本质是时空同一化,时间就是光速运动空间形成的。
按照狭义相对论,运动的时钟走得慢。
于是有人设想,双生子甲和乙一出生时候,甲就乘高速飞船到远方宇宙空间去旅行,双生子乙则留在地球上,经过若干年飞船返回地球。
按地球上的乙看来,甲处于运动之中,甲的生命过程进行得缓慢,则甲比乙年轻;
而按飞船上的甲看来,乙是运动的,则乙比较年轻。
重返相遇的比较,结果应该是唯一的,似乎狭义相对论遇到无法克服的难题。
对双生子佯谬的解释,无论的拥护相对论或是反对相对论的人,解释都比较混乱。
按照统一场论的看法,描述和计算一个运动过程,需要确定观察者,确定开始时刻和地点,以及结束的时刻和地点。
不确定观察者、开始和结束的时刻、地点,讨论运动的结果是没有意义的。
双生子问题中,甲和乙开始分手,到最后甲乙碰面的地点,都在地球上,所以,地球可以作为参考点。
由于甲相对于地球是运动的,所以,甲比乙年轻。乙相对于地球是静止的,乙的时间是固有时。
如果甲和乙诞生于太空中,拥抱在一起,后来,二人分手,没有地球作为参考点?我们怎么判断?
这个时候,需要确定两个人,是哪一个开始加速运动,离开对方的。
这个其实涉及到了一个关于运动的根本问题——物体的运动状态的改变【也就是加速度】是有原因的,物体不会无缘无故的改变运动速度【包括从速度为零的静止状态加速到某一个速度】。也就是本来拥抱在一起的甲、乙二人,不会无缘无故的分开。
设想在某一个时刻,是甲开始加速运动离开了乙,甲转了一圈回来,二人相遇,则甲年轻。
如果在太空中,甲乙二人拥抱在一起,后来相互踹对方一脚,二人都以相同的力,完全相同的踹法,彼此离开,在宇宙空间转一圈后相遇,谁更年轻?
这种情况下,甲乙二人应该是同样的年轻。
Learn